题目内容
 如图,已知菱形ABCD中,∠ABC=60°,点E在边BC上,∠BAE=25°.把线段AE绕点A逆时针方向旋转,使点E落在边DC上,则旋转角α的度数为________.
如图,已知菱形ABCD中,∠ABC=60°,点E在边BC上,∠BAE=25°.把线段AE绕点A逆时针方向旋转,使点E落在边DC上,则旋转角α的度数为________.
60°或70°
分析:连接AC,根据菱形的性质及等边三角形的判定易证△ABC是等边三角形.分两种情况:①将△ABE绕点A逆时针旋转60°,点E可落在边DC上,此时△ABE与△ABE1重合;②将线段AE绕点A逆时针旋转70°,点E可落在边DC上,点E与点E2重合,此△AEC≌△AE2C.
解答:连接AC.
∵菱形ABCD中,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∴∠ACD=60°.
本题有两种情况:
①如图,将△ABE绕点A逆时针旋转,使点B与点C重合,点E与点E1重合,此时△ABE≌△ABE1,AE=AE1,旋转角α=∠BAC=60°;

②∵∠BAC=60°,∠BAE=25°,
∴∠EAC=35°.
如图,将线段AE绕点A逆时针旋转70°,使点E到点E2的位置,
此时△AEC≌△AE2C,AE=AE2,旋转角α=∠EAE2=70°.

综上可知,符合条件的旋转角α的度数为60度或70度.
点评:本题主要考查了菱形的性质、等边三角形的判定,旋转的定义及性质.本题容易漏掉第二种情况.
分析:连接AC,根据菱形的性质及等边三角形的判定易证△ABC是等边三角形.分两种情况:①将△ABE绕点A逆时针旋转60°,点E可落在边DC上,此时△ABE与△ABE1重合;②将线段AE绕点A逆时针旋转70°,点E可落在边DC上,点E与点E2重合,此△AEC≌△AE2C.
解答:连接AC.
∵菱形ABCD中,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∴∠ACD=60°.
本题有两种情况:
①如图,将△ABE绕点A逆时针旋转,使点B与点C重合,点E与点E1重合,此时△ABE≌△ABE1,AE=AE1,旋转角α=∠BAC=60°;

②∵∠BAC=60°,∠BAE=25°,
∴∠EAC=35°.
如图,将线段AE绕点A逆时针旋转70°,使点E到点E2的位置,
此时△AEC≌△AE2C,AE=AE2,旋转角α=∠EAE2=70°.

综上可知,符合条件的旋转角α的度数为60度或70度.
点评:本题主要考查了菱形的性质、等边三角形的判定,旋转的定义及性质.本题容易漏掉第二种情况.

练习册系列答案
相关题目
 如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
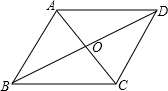 如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
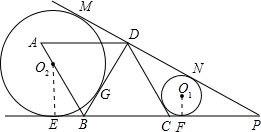 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.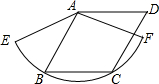 如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的
如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的