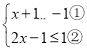题目内容
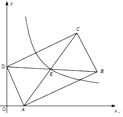
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE.
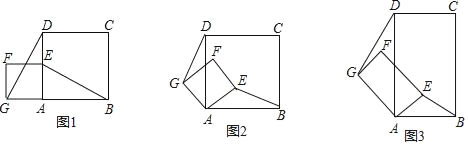
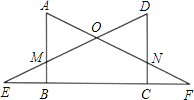
(1)发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是 ;②直线DG与直线BE之间的位置关系是 .
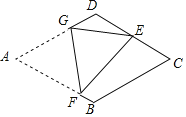
(2)探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.
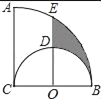
(3)应用:在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
【答案】(1)BE=DG,BE⊥DG;(2)证明见解析;(3)![]()
【解析】
(1)先判断出△ABE≌△ADG,进而得出BE=DG,∠ABE=∠ADG,再利用等角的余角相等即可得出结论;
(2)先利用两边对应成比例夹角相等判断出△ABE∽△ADG,得出∠ABE=∠ADG,再利用等角的余角相等即可得出结论;
(3)先求出BE,进而得出BE=AB,即可得出四边形ABEG是平行四边形,进而得出∠AEB=90°,求出BE,借助(2)得出的相似,即可得出结论.
(1)①∵四边形ABCD和四边形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△ADG中,
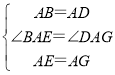 ,
,
∴△ABE≌△ADG(SAS),
∴BE=DG;
②如图2,延长BE交AD于G,交DG于H,
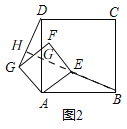
由①知,△ABE≌△ADG,
∴∠ABE=∠ADG,
∵∠AGB+∠ABE=90°,
∴∠AGB+∠ADG=90°,
∵∠AGB=∠DGH,
∴∠DGH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG
(2)∵四边形ABCD与四边形AEFG都为矩形,
∴∠BAD=∠DAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴![]() ,
,
∴△ABE∽△ADG,
∴∠ABE=∠ADG,
∵∠AGB+∠ABE=90°,
∴∠AGB+∠ADG=90°,
∵∠AGB=∠DGH,
∴∠DGH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG;
(3)如图4,(为了说明点B,E,F在同一条线上,特意画的图形)
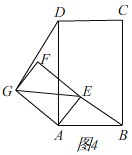
∵EG∥AB,
∴∠DME=∠DAB=90°,
在Rt△AEG中,AE=1,
∴AG=2AE=2,
根据勾股定理得,EG=![]() ,
,
∵AB=![]() ,
,
∴EG=AB,
∵EG∥AB,
∴四边形ABEG是平行四边形,
∴AG∥BE,
∵AG∥EF,
∴点B,E,F在同一条直线上如图5,
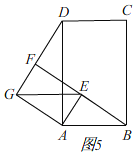
∴∠AEB=90°,
在Rt△ABE中,根据勾股定理得,BE=![]() =2,
=2,
由(3)知,△ABE∽△ADG,
∴![]() ,
,
∴![]() ,
,
∴DG=4.