题目内容
 如图,O为平行四边形ABCD对角线AC、BD的交点,EF经过点O,且与边AD、BC分别交于点E、F,若BF=DE,则图中的全等三角形最多有
如图,O为平行四边形ABCD对角线AC、BD的交点,EF经过点O,且与边AD、BC分别交于点E、F,若BF=DE,则图中的全等三角形最多有
- A.8对
- B.6对
- C.5对
- D.4对
B
分析:根据平行四边形的性质推出AD=BC,AB=CD,OA=OC,OD=OB,根据SSS能推出△ABD≌△CDB,△ABC≌△CDA;根据SAS推出△AOD≌△COB,△AOB≌△COD;根据平行线的性质推出∠AEO=∠CFO,∠DEO=∠BFO,根据AAS能推出△AOE≌△COF,△DOE≌△BOF.
解答:共6对,有△ABD≌△CDB,△ABC≌△CDA,△AOD≌△COB,△AOB≌△COD,△AOE≌△COF,△DOE≌△BOF,
理由是:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵在△ABC和△CDA中
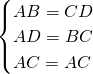 ,
,
∴△ABC≌△CDA,
同理△ABD≌△CDB,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵在△AOD和△COB中
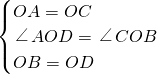 ,
,
∴△AOD≌△COB,
同理,△AOB≌△COD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEO=∠CFO,
∵在△AOE和△COF中
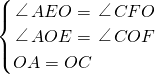 ,
,
∴△AOE≌△COF,
同理,△DOE≌△BOF,
故选B.
点评:本题考查了平行四边形性质,平行线性质,全等三角形的判定的应用,注意:平行四边形的对边平行且相等,平行四边形的对角线互相平分,全等三角形的判定方法有SAS,ASA,AAS,SSS等,本题主要考查了学生运用定理进行推理的能力.
分析:根据平行四边形的性质推出AD=BC,AB=CD,OA=OC,OD=OB,根据SSS能推出△ABD≌△CDB,△ABC≌△CDA;根据SAS推出△AOD≌△COB,△AOB≌△COD;根据平行线的性质推出∠AEO=∠CFO,∠DEO=∠BFO,根据AAS能推出△AOE≌△COF,△DOE≌△BOF.
解答:共6对,有△ABD≌△CDB,△ABC≌△CDA,△AOD≌△COB,△AOB≌△COD,△AOE≌△COF,△DOE≌△BOF,
理由是:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∵在△ABC和△CDA中
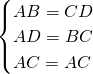 ,
,∴△ABC≌△CDA,
同理△ABD≌△CDB,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵在△AOD和△COB中
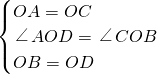 ,
,∴△AOD≌△COB,
同理,△AOB≌△COD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEO=∠CFO,
∵在△AOE和△COF中
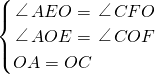 ,
,∴△AOE≌△COF,
同理,△DOE≌△BOF,
故选B.
点评:本题考查了平行四边形性质,平行线性质,全等三角形的判定的应用,注意:平行四边形的对边平行且相等,平行四边形的对角线互相平分,全等三角形的判定方法有SAS,ASA,AAS,SSS等,本题主要考查了学生运用定理进行推理的能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
 如图,E为平行四边形ABCD中BC边的中点,AE交对角线BD于G,如果△BEG的面积是1,则平行四边形ABCD的面积是
如图,E为平行四边形ABCD中BC边的中点,AE交对角线BD于G,如果△BEG的面积是1,则平行四边形ABCD的面积是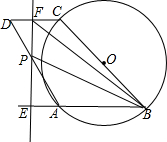 如图,ABCD为平行四边形,以BC为直径的⊙O经过点A,∠D=60°,BC=2,一动点P在AD上移动,过点P作直线AB的垂线,分别交直线AB、CD于E、F,设点O到EF的距离为t,若B、P、F三点能构成三角形,设此时△BPF的面积为S.
如图,ABCD为平行四边形,以BC为直径的⊙O经过点A,∠D=60°,BC=2,一动点P在AD上移动,过点P作直线AB的垂线,分别交直线AB、CD于E、F,设点O到EF的距离为t,若B、P、F三点能构成三角形,设此时△BPF的面积为S.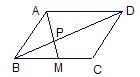 14、如图:M为平行四边形ABCD的BC边的中点,AM交BD于点P,若PM=4,则AP=
14、如图:M为平行四边形ABCD的BC边的中点,AM交BD于点P,若PM=4,则AP= (2013•安徽)如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=
(2013•安徽)如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=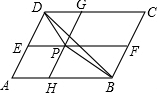 (1)已知|2011-x|+
(1)已知|2011-x|+