题目内容
如图,⊙O的直径AB垂直于弦CD,垂足为H,点P是 上一点(点P不与A、C两点重合),连接PC、PD
上一点(点P不与A、C两点重合),连接PC、PD 、PA、AD,点E在AP的延长线上,PD与AB交于点F,给出下列四个结论:
、PA、AD,点E在AP的延长线上,PD与AB交于点F,给出下列四个结论:
(1)CH2=AH•BH;
(2)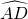 =
= ;
;
(3)AD2=DF•DP;
(4)∠EPC=∠APD,其中正确的个数是
- A.1
- B.2
- C.3
- D.4
C
分析:根据圆周角定理,垂径定理,圆内接四边形的性质,相交弦定理,采用排除法,逐条分析判断.
解答: 解:由垂径定理知,点H是CD的中点,
解:由垂径定理知,点H是CD的中点, =
= ,故(2)正确;
,故(2)正确;
弧AC对的圆周角为∠ADC,弧AD对的圆周角为∠APD,
∴∠ADC=∠APD,
由圆内接四边形的外角等于它的内对角知,∠EPC=∠ADC,
∴∠EPC=∠APD,故(4)正确;
由相交弦定理知,CH•HD=CH2=AH•BH,故(1)正确;
连接BD后,可得AD2=AH•AB,故(3)不正确,所以选项C正确.
故选C.
点评:本题利用了圆周角定理,垂径定理,圆内接四边形的性质,相交弦定理求解.
分析:根据圆周角定理,垂径定理,圆内接四边形的性质,相交弦定理,采用排除法,逐条分析判断.
解答:
 解:由垂径定理知,点H是CD的中点,
解:由垂径定理知,点H是CD的中点, =
= ,故(2)正确;
,故(2)正确;弧AC对的圆周角为∠ADC,弧AD对的圆周角为∠APD,
∴∠ADC=∠APD,
由圆内接四边形的外角等于它的内对角知,∠EPC=∠ADC,
∴∠EPC=∠APD,故(4)正确;
由相交弦定理知,CH•HD=CH2=AH•BH,故(1)正确;
连接BD后,可得AD2=AH•AB,故(3)不正确,所以选项C正确.
故选C.
点评:本题利用了圆周角定理,垂径定理,圆内接四边形的性质,相交弦定理求解.

练习册系列答案
相关题目
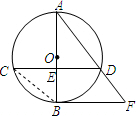 已知:如图,⊙O的直径AB与弦CD相交于E,
已知:如图,⊙O的直径AB与弦CD相交于E,
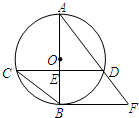 如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于
如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于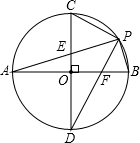 如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:
如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论: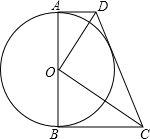 (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=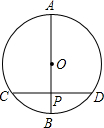 如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是
如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是