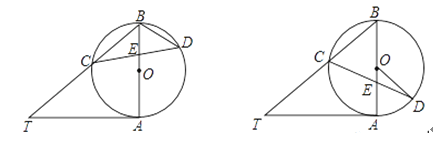题目内容
【题目】已知⊙O是等边三角形ABC的外接圆,P为劣弧BC上一点(点P与点B,C不重合).
(1)如果P是劣弧BC的中点,求证:PB+PC=PA;
(2)当点P在劣弧BC上移动时,(1)中的结论还成立吗?请说明理由.
【答案】(1)证明见解析(2)成立
【解析】(1)连接OB,OC,由P是劣弧BC的中点,得PB=PC,由△ABC为等边三角形知![]() ,故可证AP是⊙P的直径, 易证△OBP和△OPC是等边三角形,从而可证明PB+PC=PA;
,故可证AP是⊙P的直径, 易证△OBP和△OPC是等边三角形,从而可证明PB+PC=PA;
(2)在弦PA上截取PE=PC,连接CE.证明△CAE≌△CBP即可得出结论
(1)证明:如图①,连接OB,OC.
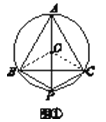
∵△ABC是⊙O的内接等边三角形,
∴AB=AC,
∴![]() ,
,
∵P是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴AP为⊙O的直径.
∵∠BPO=∠BCA=60°,且OB=OP,
∴△OBP是等边三角形,
同理△OPC是等边三角形,
∴PB=PC=OP=OA,
∴PB+PC=PA.
(2)(1)中的结论还成立.理由如下:
如图②,在弦PA上截取PE=PC,连接CE.

∵∠APC=∠ABC=60°,
∴△PEC为等边三角形,
∴CE=CP.
∵∠PCE=60°,且∠ACB=60°,
∴∠ACE=∠BCP.
又∵CA=CB,
∴△CAE≌△CBP,
∴AE=PB.
∵AE+PE=PA,
∴PB+PC=PA.

练习册系列答案
相关题目