题目内容
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
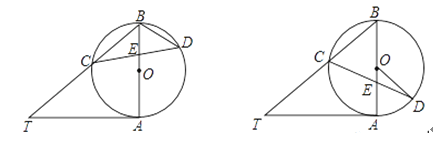
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC,求∠CDO的大小.
【答案】(1)∠T==40°,∠CDB=40°;(2)∠CDO=15°.
【解析】试题分析:(1)根据切线的性质:圆的切线垂直于经过切点的半径,得∠TAB=90°,根据三角形内角和得∠T的度数,由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数;
(2)如图②,连接AD,根据等边对等角得:∠BCE=∠BEC=65°,利用同圆的半径相等知:OA=OD,同理∠ODA=∠OAD=65°,由此可得结论.
试题解析:(1)如图,连接AC,
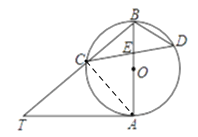
∵AB是⊙O的直径,AD是⊙O的切线,
∴AT⊥AB,即∠TAB=90°
∵∠ABT=50°,
∴∠T=90°-∠ABT=40°
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°-∠ABC=40°
∴∠CDB=∠CAB=40°;
(2)如图,连接AD
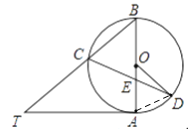
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°
∵OA=OD
∴∠ODA=∠OAD=65°
∵∠ADC=∠ABC=50°
∴∠CDO=∠ODA-∠ADC=15°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中五次行驶纪录如下。(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
-4 | +7 | -9 | +7 | -2 |
(1)求第二次记录时距A地多远?
(2)在第______次纪录时距A地最远。
(3)若每千米耗油0.8升,问共耗油多少升?