��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���M������Ϊ��x1��y1�����������Ϊ��x2��y2������x1��x2��y1��y2����MNΪ�߹������Σ��������ε������ԽǷ�ƽ����x�ᡢy�ᣬ��Ƹ�����Ϊ�ߵġ��������Ρ���

��1����֪��A��2��0����B��0��3��������ABΪ�ߵġ��������Ρ������Ϊ�� ����
��2������C��1��2������D��ֱ��x��5�ϣ���CDΪ�ߵġ��������Ρ�Ϊ�����Σ���ֱ��CD�ĺ�������ʽ��
���𰸡���1��12����2��y��x+1��y����x+3
��������
��1�����ݶ��彨����ABΪ�ߵ�����������������������������ɣ�
��2����ȷ��ֱ��CD��ֱ��y=5�ļн���45�㣬��D��5��6����5����2�������ô���ϵ������ֱ��CD����ʽ.
�⣺��1����ͼ1��
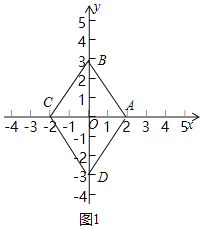
�ߵ�A��2��0����B��0��3����
��OA��2��OB��3��
���ı���ABCD������
��AC��2OA��4��BD��2OB��6��
����ABΪ�ߵġ��������Ρ��������![]() AC��BD��12��
AC��BD��12��
�ʴ�Ϊ��12
��2����ͼ2��
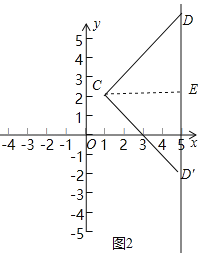
����CDΪ�ߵġ��������Ρ�Ϊ�����Σ�
��ֱ��CD��ֱ��x��5�ļн���45�㣬
����C��CE��DE��E��
��D��5��6����5����2����
��ֱ��CD�Ľ���ʽΪy��kx+b��
![]() ��
��![]()
��![]() ��
��![]()
��ֱ��CD�ı���ʽΪ��y��x+1��y����x+3��

 �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�����Ŀ��(10�֣�ѧУ��֯ѧ���μ��ۺ�ʵ��������Dz�����ij��Ʒ���˶�Ь�����۹�������֪���˶�Ьÿ˫�Ľ���Ϊ120Ԫ��ΪѰ����ʵ����ۼ۸������4�������������������±���ʾ��
��1�� | ��2�� | ��3�� | ��4�� | |
�ۼ�x��Ԫ/˫�� | 150 | 200 | 250 | 300 |
������y��˫�� | 40 | 30 | 24 | 20 |
��1���۲�������ݣ�x��y����ʲô������ϵ����������������ϵʽ��
��2�����̳��ƻ�ÿ�����������Ϊ3000Ԫ�����䵥�۶�Ϊ����Ԫ��