题目内容
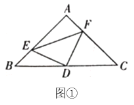
【题目】如图,矩形ABCD中,BC=4,且AB=![]() ,连接对角线AC,点E为AC中点,点F为线段AB上的动点,连接EF,作点C关于EF的对称点C',连接C'E,C'F,若△EFC'与△ACF的重叠部分(△EFG)面积等于△ACF的
,连接对角线AC,点E为AC中点,点F为线段AB上的动点,连接EF,作点C关于EF的对称点C',连接C'E,C'F,若△EFC'与△ACF的重叠部分(△EFG)面积等于△ACF的![]() ,则BF=________.
,则BF=________.
【答案】2![]() -
-![]()
【解析】
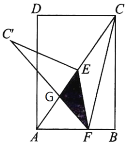
连接C′E,C′A,作EM⊥BC于M,EN⊥PC′于N.只要证明四边形AFEC′是平行四边形即可解决问题.
解:连接C′E,C′A,作EM⊥CF于M,EN⊥FC′于N.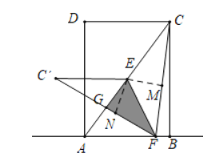
∵△EFC′与△ACF的重叠部分(△EFG)面积等于△ACF的![]() ,
,
∴EG=AG,
∵∠EFC=∠EFC′,EM⊥BC于M,EN⊥FC′于N,
∴EM=EN,
∴![]() =
=![]() =
=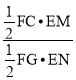 =2,
=2,
∴FC=2FG,
∵FC′=FC,
∴FG=C′G,∵AG=GE,
∴四边形AFEC′是平行四边形,
∴EC′=AF=EC=![]() AC=
AC=![]() ×
×![]() =
=![]() ,
,
∴FB=2![]() -
-![]() .
.
故答案为2![]() -
-![]() .
.

练习册系列答案
相关题目