题目内容
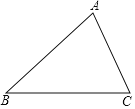
【题目】(1)如图1,在⊙O中,弦AB与CD相交于点F,∠BCD=68°,∠CFA=108°,求∠ADC的度数.
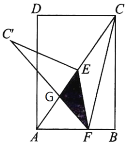
(2)如图2,在正方形ABCD中,点E是CD上一点(DE>CE),连接AE,并过点E作AE的垂线交BC于点F,若AB=9,BF=7,求DE长.

【答案】(1)40°;(2)6.
【解析】
(1)由∠BCD=68°,∠CFA=108°,利用三角形外角的性质,即可求得∠B的度数,然后由圆周角定理,求得答案;
(2)由正方形的性质和已知条件证明△ADE∽△ECF,根据相似三角形的性质可知:![]() ,设DE=x,则EC=9﹣x,代入计算求出x的值即可.
,设DE=x,则EC=9﹣x,代入计算求出x的值即可.
(1)∵∠BCD=68°,∠CFA=108°,
∴∠B=∠CFA﹣∠BCD=108°﹣68°=40°,
∴∠ADC=∠B=40°.
(2)解:∵四边形ABCD是正方形,
∴CD=AD=BC=AB=9,∠D=∠C=90°,
∴CF=BC﹣BF=2,
在Rt△ADE中,∠DAE+∠AED=90°,
∵AE⊥EF于E,
∴∠AED+∠FEC=90°,
∴∠DAE=∠FEC,
∴△ADE∽△ECF,
∴![]() ,
,
设DE=x,则EC=9﹣x,
∴![]() ,
,
解得x1=3,x2=6,
∵DE>CE,
∴DE=6.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】![]() ,
,![]() 两地相距
两地相距![]() .甲、乙两人都由
.甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]() .
.
(1)根据题意,填写下表:
时间 与 | 0.5 | 1.8 | ______ |
甲与 | 5 | ______ | 20 |
乙与 | 0 | 12 | ______ |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() ,写出
,写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?