题目内容
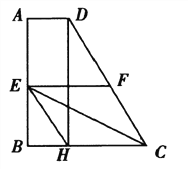
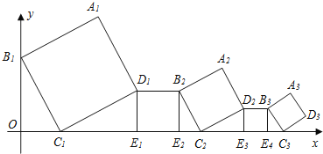
【题目】如图,正方形![]() 的边长为4,延长
的边长为4,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边在上方作正方形
为边在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() 、
、![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
由正方形的性质可得∠BAD=∠C=∠E=∠EFB=∠BGF=90°,AD//BC,继而可得四边形CEFM是矩形,∠AGF=90°,由此可得AH=FG,再根据∠NAH=∠NGF,∠ANH=∠GNF,可得△ANH≌△GNF(AAS),由此可判断①正确;由AF≠AH,判断出∠AFN≠∠AHN,即∠AFN≠∠HFG,由此可判断②错误;证明△AHK∽△MFK,根据相似三角形的性质可对③进行判断;分别求出S△ANF、S△AMD的值即可对④作出判断.
∵四边形ABCD、BEFG是正方形,
∴∠BAD=∠C=∠E=∠EFB=∠BGF=90°,AD//BC,
∴四边形CEFM是矩形,∠AGF=180°-∠BGF=90°
∴FM=EC,CM=EF=2,FM//EC,
∴AD//FM,DM=2,
∵H为AD中点,AD=4,
∴AH=2,
∵FG=2,
∴AH=FG,
∵∠NAH=∠NGF,∠ANH=∠GNF,
∴△ANH≌△GNF(AAS),故①正确;
∴∠NFG=∠AHN,NH=FN,AN=NG,
∵AF>FG,
∴AF≠AH,
∴∠AFN≠∠AHN,即∠AFN≠∠HFG,故②错误;
∵EC=BC+BE=4+2=6,
∴FM=6,
∵AD//FM,
∴△AHK∽△MFK,
∴![]() ,
,
∴FK=3HK,
∵FH=FK+KH,FN=NH,FN+NH=FH,
∴FN=2NK,故③正确;
∵AN=NG,AG=AB-BG=4-2=2,
∴AN=1,
∴S△ANF=![]() ,S△AMD=
,S△AMD=![]() ,
,
∴S△ANF:S△AMD=1:4,故④正确,
故选 C.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案