题目内容
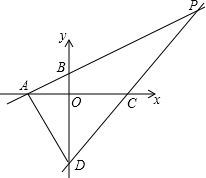 如图所示,直线AB:y=
如图所示,直线AB:y= x+1分别与x轴、y轴交于A、B两点,直线CD:y=x+b分别与x轴、y轴交于C和D.直线AB和CD相交于点P,已知△ABD的面积为4,则点P的坐标是
x+1分别与x轴、y轴交于A、B两点,直线CD:y=x+b分别与x轴、y轴交于C和D.直线AB和CD相交于点P,已知△ABD的面积为4,则点P的坐标是
- A.(3,
 )
) - B.(
 ,
, )
) - C.(4,3)
- D.(8,5)
D
分析:先求出A点坐标(-2,0),B点坐标(0,1),D点坐标(0,b),再根据△ABD的面积为4得到 ×2×(1-b)=4,解得b=-3,然后解方程组
×2×(1-b)=4,解得b=-3,然后解方程组 可确定P点坐标.
可确定P点坐标.
可得到
解答:对于y= x+1,令x=0,则y=1,所以B点坐标为(0,1),令y=0,
x+1,令x=0,则y=1,所以B点坐标为(0,1),令y=0, x+1=0,解得x=-2,所以A点坐标为(-2,0);对于y=x+b,令x=0,则y=b,所以D点坐标为(0,b),
x+1=0,解得x=-2,所以A点坐标为(-2,0);对于y=x+b,令x=0,则y=b,所以D点坐标为(0,b),
∴S△ABD= ×2×(1-b)=4,解得b=-3,
×2×(1-b)=4,解得b=-3,
∴直线CD的解析式为y=x-3,
解方程组 得
得 ,
,
∴P点坐标为(8,5).
点评:本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.
分析:先求出A点坐标(-2,0),B点坐标(0,1),D点坐标(0,b),再根据△ABD的面积为4得到
 ×2×(1-b)=4,解得b=-3,然后解方程组
×2×(1-b)=4,解得b=-3,然后解方程组 可确定P点坐标.
可确定P点坐标.可得到
解答:对于y=
 x+1,令x=0,则y=1,所以B点坐标为(0,1),令y=0,
x+1,令x=0,则y=1,所以B点坐标为(0,1),令y=0, x+1=0,解得x=-2,所以A点坐标为(-2,0);对于y=x+b,令x=0,则y=b,所以D点坐标为(0,b),
x+1=0,解得x=-2,所以A点坐标为(-2,0);对于y=x+b,令x=0,则y=b,所以D点坐标为(0,b),∴S△ABD=
 ×2×(1-b)=4,解得b=-3,
×2×(1-b)=4,解得b=-3,∴直线CD的解析式为y=x-3,
解方程组
 得
得 ,
,∴P点坐标为(8,5).
点评:本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.

练习册系列答案
相关题目
 12、如图所示,直线AB、CD相交于点O.若OM=ON=MN,那么∠APQ+∠CQP=
12、如图所示,直线AB、CD相交于点O.若OM=ON=MN,那么∠APQ+∠CQP= 24、如图所示,直线AB与x轴交于A,与y轴交于B.
24、如图所示,直线AB与x轴交于A,与y轴交于B. 如图所示,直线AB与CD相交于点O,∠DOE=60°,∠BOE=27°,求∠BOD,∠AOD,∠AOC的度数.
如图所示,直线AB与CD相交于点O,∠DOE=60°,∠BOE=27°,求∠BOD,∠AOD,∠AOC的度数. 如图所示,直线AB、CD相交于点O,∠BOD=40°,OA平分∠EOC,则∠EOD的度数为
如图所示,直线AB、CD相交于点O,∠BOD=40°,OA平分∠EOC,则∠EOD的度数为 如图所示,直线AB、CD、EF相交于点O,且EF⊥CD,若∠AOE=30°,则∠AOC=
如图所示,直线AB、CD、EF相交于点O,且EF⊥CD,若∠AOE=30°,则∠AOC=