题目内容
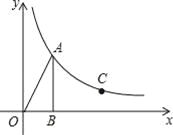
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点B在x轴的正半轴上,已知∠OBA=90°,OB=3,sin∠AOB=![]() .反比例函数y=
.反比例函数y=![]() (x>0)的图象经过点A.
(x>0)的图象经过点A.
(1)求反比例函数的解析式;
(2)若点C(m,2)是反比例函数y=![]() (x>0)图象上的点,则在x轴上是否存在点P,使得PA+PC最小?若存在,求出点P的坐标;若不存在,说明理由.
(x>0)图象上的点,则在x轴上是否存在点P,使得PA+PC最小?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)、y=![]() ;(2)、(5,0).
;(2)、(5,0).
【解析】试题分析:(1)、首先求得点A的坐标,然后利用待定系数法求反比例函数的解析式即可;(2)、首先求得点A关于x轴的对称点的坐标,然后求得直线A′C的解析式后求得其与x轴的交点即可求得点P的坐标.
试题解析:(1)∵∠OBA=90°,sin∠AOB=![]() ,可设AB=4a,OA=5a,
,可设AB=4a,OA=5a,
∴OB═![]() =3a,又OB=3, ∴a=1, ∴AB=4, ∴点A的坐标为(3,4),
=3a,又OB=3, ∴a=1, ∴AB=4, ∴点A的坐标为(3,4),
∵点A在其图象上,∴4=![]() ,∴k=12;∴反比例函数的解析式为y=
,∴k=12;∴反比例函数的解析式为y=![]() ;
;
(2)、在x轴上存在点P,使得PA+PC最小.理由如下:
∵点C(m,2)是反比例函数y=![]() (x>0)图象上的点,k=12, ∴2=
(x>0)图象上的点,k=12, ∴2=![]() ,
,
∴m=6,即点C的坐标为(6,2);
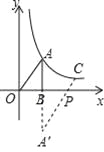
作点A(3,4)关于x轴的对称点A′(3,﹣4),如图,连结A′C.
设直线A'C的解析式为:y=kx+b, ∵A′(3,﹣4)与(6,2)在其图象上,
∴![]() ,解得
,解得![]() , ∴直线A'C的解析式为:y=2x﹣10, 令y=0,解得x=5,
, ∴直线A'C的解析式为:y=2x﹣10, 令y=0,解得x=5,
∴P(5,0)可使PA+PC最小.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目