题目内容
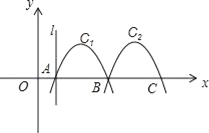
【题目】如图,抛物线C1:y=x2+4x﹣3与x轴交于A、B两点,将C1向右平移得到C2,C2与x轴交于B、C两点.
(1)求抛物线C2的解析式.
(2)点D是抛物线C2在x轴上方的图象上一点,求S△ABD的最大值.
(3)直线l过点A,且垂直于x轴,直线l沿x轴正方向向右平移的过程中,交C1于点E交C2于点F,当线段EF=5时,求点E的坐标.
【答案】(1)、y=﹣x2+8x﹣15;(2)、1;(3)、(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )
)
【解析】试题分析:(1)、先依据配方法求得抛物线C1的顶点坐标,然后令y=0,求得点A、B的坐标,从而可判断出C1平移的方向和距离,于是得到抛物线C2的顶点坐标,从而得到C2的解析式;(2)、根据函数图象可知,当点D为C2的顶点时,△ABD的面积最大;(3)、设点E的坐标为(x,﹣x2+4x﹣3),则点F的坐标为(x,﹣x2+8x﹣15),然后可求得EF长度的解析式,最后根据EF=5,可列出关于x的方程,从而可求得x的值,于是的得到点E的坐标.
试题解析:(1)、∵y=﹣x2+4x﹣3=﹣(x﹣2)2+1,∴抛物线C1的顶点坐标为(2,1).
令y=0,得﹣(x﹣2)2+1=0,解得:x1=1,x2=3.∵C2经过B,∴C1向右平移了2个单位长度.
∵将抛物线向右平移两个单位时,抛物线C2的顶点坐标为(4,1),
∴C2的解析式为y2=﹣(x﹣4)2+1,即y=﹣x2+8x﹣15.
(2)、根据函数图象可知,当点D为C2的顶点时,纵坐标最大,即D(4,1)时,△ABD的面积最大
S△ABD=![]() AB|yD|=
AB|yD|=![]() ×2×1=1.
×2×1=1.
(3)、设点E的坐标为(x,﹣x2+4x﹣3),则点F的坐标为(x,﹣x2+8x﹣15).
EF=|(﹣x2+4x﹣3)﹣(﹣x2+8x﹣15)|=|﹣4x+12|.∵EF=5,∴﹣4x+12=5或﹣4x+12=﹣5.
解得:x=![]() 或x=
或x=![]() .
.
∴点E的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )时,EF=5.
)时,EF=5.

【题目】某体育用品商店为了解5月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下两幅不完整的统计图

(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按5月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种球,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如表:
类别 | 篮球 | 足球 | 排球 |
进价(单位:元/个) | 50 | 30 | 20 |
预售价(单位:元/个) | 70 | 45 | 25 |
求出y与x之间的函数关系式;
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种球就会产生滞销
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.