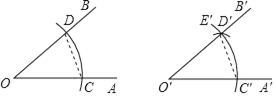��Ŀ����
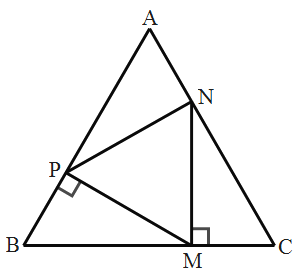
����Ŀ����ͬһƽ���ڣ�����P����ABC���������е������������������γɵ������ζ��ǵ��������Σ���Ƶ�P����ABC�������.
��1����ͼ1��������ABC�������P���߹���ͼ����д������������ͼ�ۼ���.

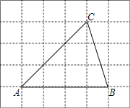
��2����ͼ2������ABC�У���A=80����AB=AC��������ABC�����������P ���߹���ͼ����д������������ͼ�ۼ�������ֱ��д����BPC�Ķ����� .

��3���ȱ������ε������ĸ����У� ��
A.2 B.6 C.10 D.12
���𰸡�(1)������;(2) 40��,160�� ��140�� ��80��;(3)C.
��������
��1�����������֪����������ij���ߵĴ�ֱƽ�����ϣ�����ֻ��Ҫ�������ߵĴ�ֱƽ�������ҵ�����㣻
��2����������ֱ���A��CΪԲ�ģ�ACΪ�뾶��Բ����BC�ߵĴ�ֱƽ���ߵĵ㼴Ϊ��P��������Բ�Ľ�����BC�ߵĴ�ֱƽ���ߵĽ���ҲΪ��P�����������ۼ������BPC�Ķ�����
��3���ֱ��Եȱ������ε����������䴹ֱƽ���ߣ��ٷֱ��Եȱ������ε���������ΪԲ�ģ��ȱ������εı߳�Ϊ�뾶��Բ���ֱ��������ߵĴ�ֱƽ���ߵĽ��㼴Ϊ�ȱ������ε������.
�⣺��1����BC�ߵĴ�ֱƽ���ߣ��ֱ���B��CΪԲ�ģ�����![]() �ij�Ϊ�뾶������������Բ���Ľ��㣻
�ij�Ϊ�뾶������������Բ���Ľ��㣻
ͬ����AB�ߵĴ�ֱƽ���ߣ��ֱ���A��BΪԲ�ģ�����![]() �ij�Ϊ�뾶��������Բ���Ľ��㣻
�ij�Ϊ�뾶��������Բ���Ľ��㣻
AB�ߵĴ�ֱƽ������BC�ߵĴ�ֱƽ���ߵĽ��㼴Ϊ�����P.

���P����.
��2����BC���ϵĴ�ֱƽ���ߣ��ٷֱ���A��CΪԲ�ģ�ACΪ�뾶��Բ����BC�ߵĴ�ֱƽ���ߵĽ��������������Ϊ![]() ,������Բ�Ľ��㣬��CB�ߵĴ�ֱƽ���ߵĽ���Ϊ
,������Բ�Ľ��㣬��CB�ߵĴ�ֱƽ���ߵĽ���Ϊ![]() ��
��![]() ������.
������.

�ٽ�![]() ,
,
��![]() ,
,
��![]() ,
,
��![]()
��![]() ��
��
������![]() ,
,
��![]() ��AC��BC�ߵĴ�ֱƽ���ߵĽ��㣬
��AC��BC�ߵĴ�ֱƽ���ߵĽ��㣬
��![]()
��![]() ,
,![]()
����![]()
�۽� ![]() ,
,
��![]() ,
,![]() ΪBC���ϵĴ�ֱƽ���ߣ�
ΪBC���ϵĴ�ֱƽ���ߣ�
��![]()
��![]() ,
,
��![]()
��![]() ��
��
������![]() ��
��
��![]() ,
,![]() ,
,![]() ΪBC���ϵĴ�ֱƽ����,
ΪBC���ϵĴ�ֱƽ����,
��![]() ,
,
��![]() ,
,![]() ��
��
��������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() .
.
��3���ֱ��Եȱ������ε������������Ӧ�ߵĴ�ֱƽ���ߣ��ٷֱ��Եȱ������ε���������ΪԲ�ģ��ȱ������εı߳�Ϊ�뾶��Բ���ֱ��������ߵĴ�ֱƽ���ߵĽ����������ֱƽ���ߵĽ��㼴Ϊ�ȱ������ε������.����ͼ�������P��10������ѡC.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�