题目内容
【题目】如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=-![]() x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.点P是y轴上一点.
x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.点P是y轴上一点.

(1)写出下列各点的坐标:点A( , )、点B( , )、点C( , );
(2)若S△COP=S△COA,请求出点P的坐标;
(3)当PA+PC最短时,求出直线PC的解析式.
【答案】(1)A(6,0),B(0,3),C(2,2);(2) P(0,![]() );(3)直线PC的解析式为
);(3)直线PC的解析式为![]()
【解析】
(1)x=0代入![]() ,即可求出点A坐标,把y=0代入
,即可求出点A坐标,把y=0代入![]() 即可求出点B坐标,求方程组
即可求出点B坐标,求方程组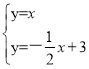 的解即可求出点C的坐标;
的解即可求出点C的坐标;
(2)设P点坐标为(0,y),根据S△COP=S△COA列方程求解即可,
(3)作点C关于y轴的对称点为M(﹣2,2),求出过点A,M的直线解析式,再求直线AM与y轴的交点坐标,即求出P的坐标,即可求出直线PC的解析式.
(1)把x=0代入![]() ,
,
∴y=3,∴B(0,3),
把y=0代入![]() ,∴x=6,A(6,0),
,∴x=6,A(6,0),
且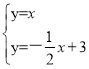 ,∴C点坐标为(2,2),
,∴C点坐标为(2,2),
(2)∵A(6,0),C(2,2)∴S△COA,=6×2÷2=6;
∵P是y轴上一点,∴设P的坐标为(0,y),
∴S△COP=![]() ,∵S△COP=S△COA,
,∵S△COP=S△COA,
∴![]() =6,∴y=±6,
=6,∴y=±6,
∴P(0,6)或(0,﹣6).
(3)如图,过点C作y轴的对称点M,连接AM与y轴交与点P,则此时PA+PC最短,

∵C的坐标为C(2,2),∴点C关于y轴的对称点为M(﹣2,2),
∴过点A,M的直线解析式为 ![]() ,
,
∵直线AM与y轴的交点为P(0,![]() ),
),
∴当P点坐标为(0,![]() )时,PA+PC最短,
)时,PA+PC最短,
∴直线PC的解析式为![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目





