题目内容
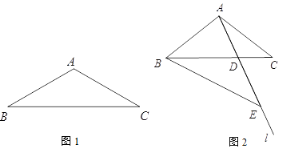
【题目】如图,在Rt直角△ABC中,∠BAC=90°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,则下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是_______________.

【答案】①②③
【解析】
根据等腰直角三角形的性质可得∠CAD=∠B=45°,根据同角的余角相等求出∠ADF=∠BDE,然后利用“角边角”证明△BDE和△ADF全等,判断出③正确;根据全等三角形对应边相等可得DE=DF、BE=AF,从而得到△DEF是等腰直角三角形,判断出①正确;再求出AE=CF,判断出②正确;根据BE+CF=AF+AE,利用三角形的任意两边之和大于第三边可得BE+CF>EF,判断出④错误.
解:∵∠B=45°,AB=AC,
∴△ABC是等腰直角三角形,
∵点D为BC中点,
∴AD=CD=BD,AD⊥BC,∠CAD=45°,
∴∠CAD=∠B,
∵∠MDN是直角,
∴∠ADF+∠ADE=90°,
∵∠BDE+∠ADE=∠ADB=90°,
∴∠ADF=∠BDE,
在△BDE和△ADF中,
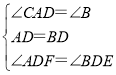 ,
,
∴△BDE≌△ADF(ASA),
故③正确;
∴DE=DF、BE=AF,
∴△DEF是等腰直角三角形,
故①正确;
∵AE=AB-BE,CF=AC-AF,
∴AE=CF,
故②正确;
∵BE+CF=AF+AE
∴BE+CF>EF,
故④错误;
综上所述,正确的结论有①②③.

练习册系列答案
相关题目