题目内容
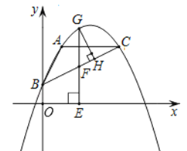
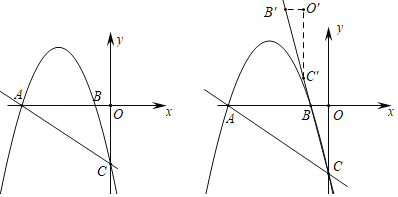
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2﹣
x2﹣![]() x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
(1)求直线AC的解析式;
(2)点P是直线AC上方抛物线上的一动点(不与点A,点C重合),过点P作PD⊥x轴交AC于点D,求PD的最大值;
(3)将△BOC沿直线BC平移,点B平移后的对应点为点B′,点O平移后的对应点为点O′,点C平移后的对应点为点C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,求出所有符合条件的点S的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)(
;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() )
)
【解析】
(1)![]() ,令y=0,则x=-1或-6,故点A、B、C的坐标分别为:(-6,0)、(-1,0)、(0,-3),然后用待定系数法即可求解;(2)设点P(x,
,令y=0,则x=-1或-6,故点A、B、C的坐标分别为:(-6,0)、(-1,0)、(0,-3),然后用待定系数法即可求解;(2)设点P(x,![]() ),则点D(x,
),则点D(x,![]() ),则PD=
),则PD=![]() -(
-(![]() )=
)=![]() ,然后配方法分析其最值,即可求解;(3)分AC是菱形的边、AC是对角线两种情况,分别求解即可.
,然后配方法分析其最值,即可求解;(3)分AC是菱形的边、AC是对角线两种情况,分别求解即可.
解:(1)当y=0时,![]()
解得:x=-1或-6,
当x=0时,y=-3
∴点A、B、C的坐标分别为:(-6,0)、(-1,0)、(0,-3),
设直线AC的表达式为:![]()
将点A、C的坐标代入得:![]()
解得: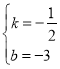
∴直线AC的解析式为:![]()
(2)设点P(x,![]() ),则点D(x,
),则点D(x,![]() )
)
则PD=![]() -(
-(![]() )=
)=![]()
∵![]() <0,故PD有最大值为
<0,故PD有最大值为![]()
(3)设直线BC的表达式为:![]()
将点B、C的坐标代入得:![]()
解得:![]()
∴直线BC的解析式为:![]()
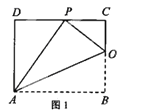
①如图3或4中,当四边形ACSO'是菱形时,设AS交CO′于K,AC=AO′=3![]() ,
,
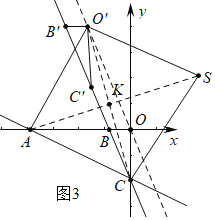
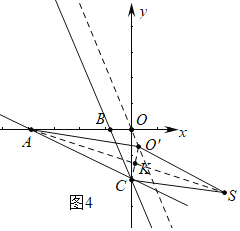
点O平移后的对应点为点O′,平移直线的k为![]() ,
,
则设点O向左平移m个单位,则向上平移3m个单位,则点O′(-m,3m),设点S(a,b),
∴(m+6)2+(-3m)2=(3![]() )2,
)2,
解得m=![]() ,
,
∴O′(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
由中点公式可得:K(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
∵AK=KS,
∴S(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
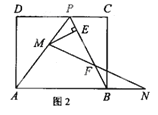
②如图5或6中,当四边形ACO'S是菱形时,设CS交AO′于K,AC=CO′=3![]() ,
,
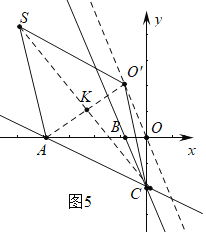
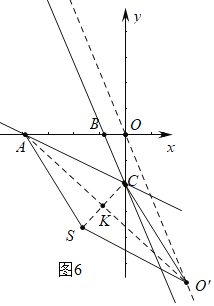
∵点O平移后的对应点为点O′,平移直线的k为![]() ,C(0,-3),设O′(m,-3m),
,C(0,-3),设O′(m,-3m),
∴m2+(-3m+3)2=(3![]() )2,
)2,
解得m=![]() ,
,
∴O′(![]() )或(
)或(![]() ),
),
由中点公式可得:K(![]() )或(
)或(![]() ),
),
∵CK=KS,
∴S(![]() )或(
)或(![]() )
)
③如图7中,当四边形ASCO′是菱形时,SO垂直平分线段AC,
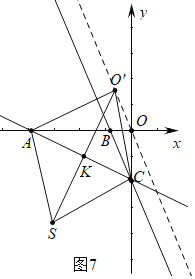
直线SO′的解析式为![]()
由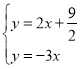 ,
,
解得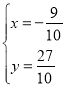 ,
,
∴O′(![]() )
)
∵KS=KO′,
∴S(![]() )
)
综上所述,满足条件的点S坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() )
)

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】嘉善县将开展以“珍爱生命,铁拳护航”为主题的交通知识竞赛,某校对参加选拔赛的若干名同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的频数统计表和扇形统计图
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合计 | 1 |
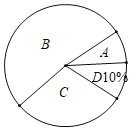
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应圆心角的度数;
(3)“A等级”的4名同学中有3名男生和1名女生,现从中随机挑选2名同学代表学校参加全县比赛,请用树状图法或列表法求出恰好选中“一男一女”的概率.