题目内容
【题目】已知,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.
(1)请你判断△DEF形状,并说明理由;
(2)若BE=2cm,CF=4cm,求EF的长.

【答案】(1)△DEF是等腰直角三角形,理由详见解析;(2)EF=2![]() cm.
cm.
【解析】
(1)连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)延长ED至G,使得DG=DE,连接FG,CG,判定△BDE≌△CDG,即可得出CG=BE=2cm,∠B=∠DCG=45°=∠ACB,利用勾股定理可得,Rt△CFG中,FG=![]() =2
=2![]() cm,再根据FD垂直平分EG,即可得到EF=GF=2
cm,再根据FD垂直平分EG,即可得到EF=GF=2![]() cm.
cm.
解:(1)△DEF是等腰直角三角形.
如图,连接AD,

∵AB=AC,∠BAC=90°,D为BC中点,
∴AD=![]() BC=BD=CD,且AD平分∠BAC,
BC=BD=CD,且AD平分∠BAC,
∴∠BAD=∠CAD=45°,
在△BDE和△ADF中,
 ,
,
∴△BDE≌△ADF(SAS),
∴DE=DF,∠BDE=∠ADF,
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,即∠EDF=90°,
∴△EDF为等腰直角三角形.
(2)如图,延长ED至G,使得DG=DE,连接FG,CG,
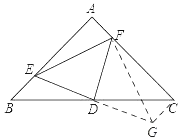
∵D为BC的中点,
∴BD=CD,
又∵∠BDE=∠CDG,
∴△BDE≌△CDG,
∴CG=BE=2cm,∠B=∠DCG=45°=∠ACB,
∴∠GCF=90°,
又∵CF=4cm,
∴Rt△CFG中,FG=![]() =
=![]() =2
=2![]() cm,
cm,
∵∠EDF=90°,ED=GD,
∴FD垂直平分EG,
∴EF=GF=2![]() cm.
cm.

 阅读快车系列答案
阅读快车系列答案




