题目内容
【题目】如图,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0,O为原点.
![]()
(1)则a= ,b= ;
(2)若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
①当PO=2PB时,求点P的运动时间t;
②当点P运动到线段OB上时,分别取AP和OB的中点E、F,则![]() 的值为 .
的值为 .
(3)有一动点Q从原点O出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点Q所对应的有理数.
【答案】(1)a=﹣2,b=6;(2)①点P的运动时间t为6或14秒;②2;(3)点Q所对应的有理数的值为﹣1008.
【解析】
试题分析:(1)根据非负数的性质即可求出a、b的值;
(2)①先表示出运动t秒后P点对应的数为﹣2+t,再根据两点间的距离公式得出PO=|﹣2+t|,PB=|﹣2+t﹣6|=|t﹣8|,利用PO=2PB建立方程,求解即可;
②根据中点坐标公式分别表示出点E表示的数,点F表示的数,再计算![]() 即可;
即可;
(3)根据题意得到点P每一次运动后所在的位置,然后由有理数的加法进行计算即可.
解:(1)∵|a+2|+(3a+b)2=0,
∴a+2=0,3a+b=0,
∴a=﹣2,b=6;
(2)①∵若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
∴运动t秒后P点对应的数为﹣2+t,
∵点A表示的数为﹣2,点B表示的数为6,
∴PO=|﹣2+t|,PB=|﹣2+t﹣6|=|t﹣8|,
当PO=2PB时,有|﹣2+t|=2|t﹣8|,
解得t=6或14.
答:点P的运动时间t为6或14秒;
②当点P运动到线段OB上时,
AP中点E表示的数是![]() =
=![]() ,OB的中点F表示的数是3,
,OB的中点F表示的数是3,
所以EF=3﹣![]() =
=![]() ,
,
则![]() =
=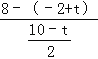 =2;
=2;
(3)依题意得:﹣1+2﹣3+4﹣5+6﹣7+…+2014﹣2015
=(﹣1+2)+(﹣3+4)+(﹣5+6))+…+(﹣2013+2014)﹣2015
=1007﹣2015
=﹣1008.
答:点Q所对应的有理数的值为﹣1008.
故答案为﹣2,6;2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案