题目内容
在△ABC和△DEF中,已知AB=DE,∠A=∠D,若要得到△ABC≌△DEF,则还要补充一个条件,在下列补充方法:①AC=DF;②∠B=∠E;③∠B=∠F;④∠C=∠F ⑤BC=EF中,错误的是
- A.①②
- B.②⑤
- C.③⑤
- D.④⑤
C
分析:根据已知条件,已知一角和一边,所以要得到两个三角形全等,可以根据角边角、角角边、边角边判定定理添加条件,而边边角不能判定两个三角形全等.
解答: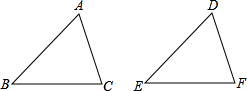 解:如图,∵AB=DE,∠A=∠D,
解:如图,∵AB=DE,∠A=∠D,
∴根据“边角边”可添加①AC=DF,
根据“角边角”可添加②∠B=∠E,
根据“角角边”可添加④∠C=∠F.
所以补充①②④可判定△ABC≌△DEF;
而∠B与∠F不是对应角,即使补充条件③∠B=∠F,也不能判定△ABC≌△DEF,
由于边边角不能判定两个三角形全等,即使补充条件⑤BC=EF,也不能判定△ABC≌△DEF.
所以补充③⑤不能判定△ABC≌△DEF.
故选C.
点评:此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有SSS,SAS,ASA,AAS,HL,注意AAA及SSA不能判定两个三角形全等.
分析:根据已知条件,已知一角和一边,所以要得到两个三角形全等,可以根据角边角、角角边、边角边判定定理添加条件,而边边角不能判定两个三角形全等.
解答:
 解:如图,∵AB=DE,∠A=∠D,
解:如图,∵AB=DE,∠A=∠D,∴根据“边角边”可添加①AC=DF,
根据“角边角”可添加②∠B=∠E,
根据“角角边”可添加④∠C=∠F.
所以补充①②④可判定△ABC≌△DEF;
而∠B与∠F不是对应角,即使补充条件③∠B=∠F,也不能判定△ABC≌△DEF,
由于边边角不能判定两个三角形全等,即使补充条件⑤BC=EF,也不能判定△ABC≌△DEF.
所以补充③⑤不能判定△ABC≌△DEF.
故选C.
点评:此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有SSS,SAS,ASA,AAS,HL,注意AAA及SSA不能判定两个三角形全等.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 20、如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明.
20、如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明.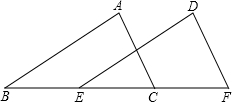 如图所示,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有六个条件,请你在其中选三个作为已知条件,余下的选一个作为结论,编写出一个真命题,并说明理由.①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF;⑤∠ACB=∠DEF;⑥∠A=∠D(填写序号即可)
如图所示,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有六个条件,请你在其中选三个作为已知条件,余下的选一个作为结论,编写出一个真命题,并说明理由.①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF;⑤∠ACB=∠DEF;⑥∠A=∠D(填写序号即可)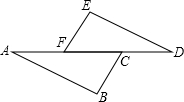 如图,已知BC∥EF,且BC=EF,AF=CD,则AB=DE,说明理由.
如图,已知BC∥EF,且BC=EF,AF=CD,则AB=DE,说明理由.