题目内容
.(本题8分)如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED.
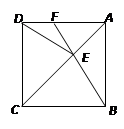
小题1:(1) 写出图中所有的全等三角形
小题2:(2) 延长BE交AD于点F,若∠DEB = 140°,求∠AFE的度数.

小题1:(1) 写出图中所有的全等三角形
小题2:(2) 延长BE交AD于点F,若∠DEB = 140°,求∠AFE的度数.
小题1:(1)△ADC≌△ABC △ADE≌△ABE △DCE≌△BCE
小题2:65°
分析:
(1)根据正方形的对称性,找出关于对角线AC对称的三角形即可;
(2)根据对称性求出∠BEC的度数,再根据正方形的对角线平分一组对角求出∠ACB=45°,然后利用三角形的内角和等于180°求出∠CBE的度数,再利用两直线平行,内错角相等求解即可。
解答:
解:(1)根据正方形的对称性,正方形ABCD关于直线AC成轴对称,
所以,全等的三角形有:△ADC≌△ABC,△ADE≌△ABE,△DCE≌△BCE;
(2)∵∠DEB=140°,
∴∠BEC=1/2∠DEB=1/2×140°=70°,
又∵正方形对角线AC平分∠BCD,
∴∠ACB=45°,
在△BCE中,∠CBE=180°-∠BEC-∠ACB=180°-70°-45°=65°,
∵AD∥BC,
∴∠AFE=∠CBE=65°。
点评:本题考查了正方形的性质,主要涉及正方形的轴对称性,两直线平行,内错角相等的性质,熟练掌握正方形的轴对称性是解题的关键。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,设其长
,设其长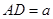 ,宽
,宽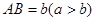 ,在
,在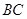 边上选取一点
边上选取一点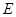 ,将△
,将△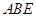 沿
沿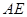 翻折后
翻折后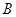 至直线
至直线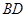 上的
上的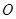 点,若
点,若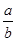 的值是_____________.
的值是_____________.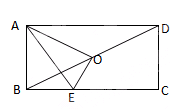
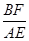 的值。
的值。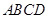 中,
中,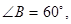 点
点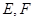 分别从点
分别从点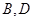 出发以同样的速度沿边
出发以同样的速度沿边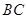 ,
,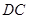 向点
向点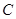 运动.给出以下四个结论:①
运动.给出以下四个结论:①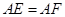 ;②
;②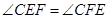 ;③当点
;③当点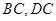 的中点时,
的中点时,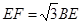 ;④当点
;④当点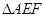 的面积最大.上述结论中正确的序号有_______.(把你认为正确的序号填在横线上)
的面积最大.上述结论中正确的序号有_______.(把你认为正确的序号填在横线上)
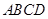 中,对角线
中,对角线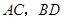 交于点
交于点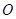 , 已知∠AOD=120°,AB=3,则
, 已知∠AOD=120°,AB=3,则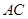 的长为 ▲ .
的长为 ▲ .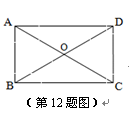
 分∠DCF.
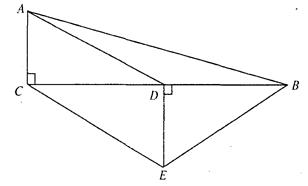
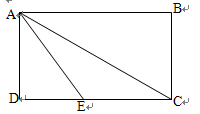
分∠DCF. 满分6分)如图,在△ABC中,∠ACB=90°,D是BC中点,DE⊥BC,CE∥AD,若AC=2,CE=4.求四边形ACEB的周长.
满分6分)如图,在△ABC中,∠ACB=90°,D是BC中点,DE⊥BC,CE∥AD,若AC=2,CE=4.求四边形ACEB的周长.