Question

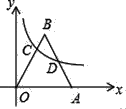
【题目】如图，在平面直角坐标系中，等边三角形OAB的顶点A的坐标为（5，0），顶点B在第一象限，函数y=（x＞0）的图象分别交边OA、AB于点C、D．若OC=2AD，则k=_____

Answer 1

【答案】4

【解析】

作CE⊥x轴于点E，DF⊥x轴于点F， CE=2DF；设OE为a，则CE=；由反比例函数k的几何意义可知△COE与△AOD面积相等，则因OC=2AD可得OF=2a；再由C和D点均在反比例函数上可求解k.

解：作CE⊥x轴于点E，DF⊥x轴于点F，

设OE为a，由题意可知△AOB为等边三角形可得CE=，则DF=，BF=；由反比例函数k的几何意义可知△COE与△AOD面积相等，则由三角形面积公式及CE=2DF可得OF=2OE=2a；由OB=5可得OF+BF=2a+=5，解得a=2，则k=2×2=4.

故答案为：4.