题目内容
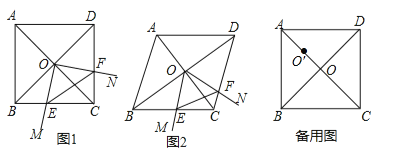
【题目】(12分)菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
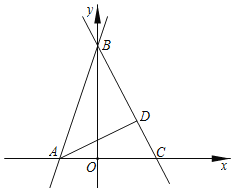
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
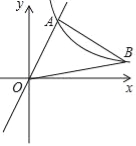
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
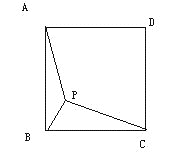
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且![]() 时,直接写出线段CE的长.
时,直接写出线段CE的长.
【答案】(1)△OEF是等腰直角三角形;(2)△OEF是等边三角形;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)先证四边形ABCD是正方形,得出∠EBO=∠FCO=45°,OB=OC,得出∠BOE=∠COF,进一步得到△BOE≌△COF,从而得到结论;
(2)过O点作OG⊥BC于G,作OH⊥CD于H,根据菱形的性质可得CA平分∠BCD,∠ABC+BCD=180°,求得OG=OH,∠BCD=120°,∠GOH=∠EOF=60°,进一步得出∠EOG=∠FOH,得出△EOG≌△FOH,从而得到结论;
(3)过O点作OG⊥BC于G,作OH⊥CD于H,先求得四边形O′GCH是正方形,从而求得GC=O′G=3,∠GO′H=90°,得到△EO′G ≌△FO′H全等,得到△O′EF是等腰直角三角形,根据已知求得等腰直角三角形的直角边O′E的长,然后根据勾股定理求得EG,即可求得CE的长.
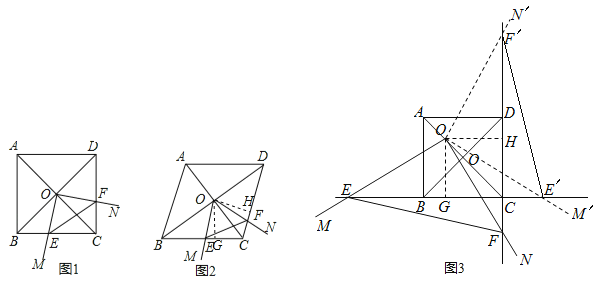
试题解析:(1)△OEF是等腰直角三角形;如图1,∵菱形ABCD中,∠ABC=90°,∴四边形ABCD是正方形,∴OB=OC,∠BOC=90°,∠BCD=90°,∠EBO=∠FCO=45°,∴∠BOE+∠COE=90°,∵∠MON+∠BCD=180°,∴∠MON=90°,∴∠COF+∠COE=90°,∴∠BOE=∠COF,在△BOE与△COF中,∵∠BOE=∠COF,OB=OC,∠EBO=∠FCO,∴△BOE≌△COF(ASA),∴OE=OF,∴△OEF是等腰直角三角形;
(2)△OEF是等边三角形;如图2,过O点作OG⊥BC于G,作OH⊥CD于H,∴∠OGE=∠OGC=∠OHC=90°,∵四边形ABCD是菱形,∴CA平分∠BCD,∠ABC+BCD=180°,∴OG=OH,∠BCD=180°﹣60°=120°,∵∠GOH+∠OGC+∠BCD+∠OHC=360°,∴∠GOH+∠BCD=180°,∴∠MON+∠BCD=180°,∴∠GOH=∠EOF=60°,∵∠GOH=∠GOF+∠FOH,∠EOF=∠GOF+∠EOG,∴∠EOG=∠FOH,在△EOG与△FOH中,∵∠EOG=∠FOH,OG=OH,∠EGO=∠FHO,∴△EOG≌△FOH(ASA),∴OE=OF,∴△OEF是等边三角形;
(3)如图3,∵菱形ABCD中,∠ABC=90°,∴四边形ABCD是正方形,∴![]() ,过O点作O′G⊥BC于G,作O′H⊥CD于H,∴∠O′GC=∠O′HC=∠BCD=90°,∴四边形O′GCH是矩形,∴O′G∥AB,O′H∥AD,∴
,过O点作O′G⊥BC于G,作O′H⊥CD于H,∴∠O′GC=∠O′HC=∠BCD=90°,∴四边形O′GCH是矩形,∴O′G∥AB,O′H∥AD,∴![]() ,∵AB=BC=CD=AD=4,∴O′G=O′H=3,∴四边形O′GCH是正方形,∴GC=O′G=3,∠GO′H=90°,∵∠MO′N+∠BCD=180°,∴∠EO′F=90°,∴∠EO′F=∠GO′H=90°,∵∠GO′H=∠GO′F+∠FO′H,∠EO′F=∠GO′F+∠EO′G,∴∠EO′G=∠FO′H,在△EO′G与△FO′H中,∵∠EO′G=∠FO′H,O′G= O′H,∠EG O′=∠FH O′,∴△EO′G≌△FO′H(ASA),∴O′E=O′F,∴△O′EF是等腰直角三角形;∵S正方形ABCD=4×4=16,
,∵AB=BC=CD=AD=4,∴O′G=O′H=3,∴四边形O′GCH是正方形,∴GC=O′G=3,∠GO′H=90°,∵∠MO′N+∠BCD=180°,∴∠EO′F=90°,∴∠EO′F=∠GO′H=90°,∵∠GO′H=∠GO′F+∠FO′H,∠EO′F=∠GO′F+∠EO′G,∴∠EO′G=∠FO′H,在△EO′G与△FO′H中,∵∠EO′G=∠FO′H,O′G= O′H,∠EG O′=∠FH O′,∴△EO′G≌△FO′H(ASA),∴O′E=O′F,∴△O′EF是等腰直角三角形;∵S正方形ABCD=4×4=16,![]() ,∴S△O′EF=18,∵S△O′EF=
,∴S△O′EF=18,∵S△O′EF=![]() ,∴O′E=6,在RT△O′EG中,EG=
,∴O′E=6,在RT△O′EG中,EG=![]() =
=![]() =
=![]() ,∴CE=CG+EG=
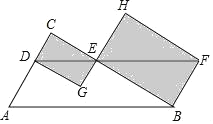
,∴CE=CG+EG=![]() .根据对称性可知,当∠M′ON′旋转到如图所示位置时,CE′=E′G﹣CG=
.根据对称性可知,当∠M′ON′旋转到如图所示位置时,CE′=E′G﹣CG=![]() .
.
综上可得,线段CE的长为![]() 或
或![]() .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案