Question

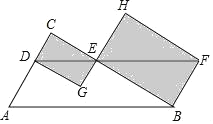
【题目】如图，在Rt△ABC中，∠C＝90°，BC＝4，BA＝5，点D是边AC上的一动点，过点D作DE∥AB交边BC于点E，过点B作BF⊥BC交DE的延长线于点F，分别以DE，EF为对角线画矩形CDGE和矩形HEBF，则在D从A到C的运动过程中，当矩形CDGE和矩形HEBF的面积和最小时，AD的长度为______．

Answer 1

【答案】

【解析】

利用勾股定理求得AC＝3，设DC＝x，则AD＝3﹣x，利用平行线分线段成比例定理求得CE＝进而求得BE＝4﹣，然后根据S阴＝S矩形CDGE+S矩形HEBF得到S阴＝x2﹣8x+12，根据二次函数的性质即可求得．

解：在Rt△ABC中，∠C＝90°，BC＝4，BA＝5，

∴AC＝＝3，

设DC＝x，则AD＝3﹣x，

∵DF∥AB，

∴＝，即＝，

∴CE＝

∴BE＝4﹣，

∵矩形CDGE和矩形HEBF，

∴AD∥BF，

∴四边形ABFD是平行四边形，

∴BF＝AD＝3﹣x，

则S阴＝S矩形CDGE+S矩形HEBF＝DCCE+BEBF＝xx+（3﹣x）（4﹣x）＝x2﹣8x+12，

∵＞0，∴当x＝﹣＝时，有最小值，

∴DC＝，有最小值，即AD＝3﹣＝时，矩形CDGE和矩形HEBF的面积和最小，

故答案为．