题目内容
【题目】如图,在直角梯形 AOBC 中,AC∥OB,且 OB=6,AC=5,OA=4.
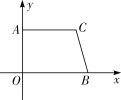
(1)求 B、C 两点的坐标;
(2)以 O、A、B、C 中的三点为顶点可组成哪几个不同的三角形?
(3)是否在边 AC 和 BC(含端点)上分别存在点 M 和点 N,使得△MON 的面积最大时,它的周长还最短?若存在,说明理由,并求出这时点 M、N 的坐标;若不存在,为什么?
【答案】(1)B点坐标为:(6,0),C点坐标为:(5,4);(2)可组成的三角形为:△AOB,△AOC,△BOC,△ABC四个不同的三角形;(3)存在,M点坐标为:(3,4),N点坐标为:(6,0),理由见解析.
【解析】
(1)根据OB=6,点B在![]() 轴可得B点坐标,再利用平行线性质结合AC=5以及OA=4进一步得出点C坐标即可;
轴可得B点坐标,再利用平行线性质结合AC=5以及OA=4进一步得出点C坐标即可;
(2)根据不在同一条直线上的三点可以组成一个三角形,得到以O、A、B、C中的三点为顶点可组成4个不同的三角形,从而得出答案;
(3)如图,过点M作MP∥OA交ON于点P,过点N作NQ∥OB,分别交OA、MP于点Q、G,则△MON的面积=△OMP的面积+△NMP的面积=![]() ,据此进一步根据题意分析讨论即可.
,据此进一步根据题意分析讨论即可.
(1)∵OB=6,,
∴B点坐标为:(6,0),
∵AC∥OB,AC=5,OA=4,
∴C点坐标为:(5,4);
(2)以 O、A、B、C 中的三点为顶点可组成的三角形为:△AOB,△AOC,△BOC,△ABC四个不同的三角形;
(3)
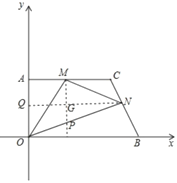
如图,过点M作MP∥OA交ON于点P,过点N作NQ∥OB,分别交OA、MP于点Q、G,
则△MON的面积=△OMP的面积+△NMP的面积=![]() ,
,
∵MP≤OA,QN≤OB,
∴当点N与点B重合,点M在AC上运动时,QN、MP同时取得最大值BO、OA,
∴△MON的最大面积=![]() ,
,
∵点N与点B重合,
∴N点坐标为(6,0),
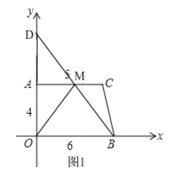
如图1,设O点关于AC的对称点为D,连接DB交AC于点M,
此时△MON的面积最大,周长最短,
∵AM∥BO,
∴![]() ,
,
即![]() ,
,
∴AM=3,
∴M点坐标为(3,4),
∴存在点M与点N,使得△MON的面积最大时,其周长最短,此时M点坐标为:(3,4),N点坐标为:(6,0).

 通城学典默写能手系列答案
通城学典默写能手系列答案