题目内容
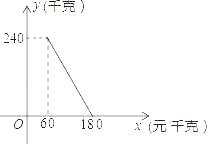
【题目】某商店以60元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系式如图所示.
(1)根据图象求出y与x的函数表达式:并写出自变量x的取值范围;
(2)当销售单价应定为多少元时,商店获得利润达到5400元?
(3)当销售单价应定为多少元时,商店获得利润最大?最大利润是多少?
【答案】(1)y与x的函数表达式:y=﹣2x+360(60≤x≤180);(2)销售单价应定为90元或150元;(3)当销售单价定为120元时,商店获得利润最大,最大探究竟7200元.
【解析】
(1)设出一次函数的一般解析式,再代入图上已知的两点坐标,求得待定系数便可;
(2)根据“(销售单价成本)×销售数量=总利润”列出方程解答便可;
(3)根据题意求出商店获得利润w与销售单价x的函数关系式,再根据函数性质求出最值便可.
解:(1)设y与x的函数解析式为y=kx+b(k≠0),则
![]() ,
,
解得,![]() ,
,
∴y与x的函数表达式:y=﹣2x+360(60≤x≤180);
(2)由题意得,y(x﹣60)=5400,
即(x﹣60)(﹣2x+360)=5400,
解得,x1=90,x2=150,
答:销售单价应定为90元或150元;
(3)商店获得利润为w,根据题意,得
w=(x﹣60)(﹣2x+360)=﹣2(x﹣120)2+7200,
∵a=﹣2<0,则抛物线开口向下,函数有最大值,
∴当x=120时,w有最大值为7200元,
答:当销售单价定为120元时,商店获得利润最大,最大探究竟7200元.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目