Question

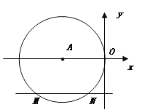
【题目】如图所示，已知⊙O的半径为2，弦BC的长为，点A为弦BC所对优弧上任意一点(B、C两点除外) (参考数据：，，．

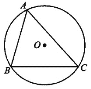
(1)求∠BAC的度数；

(2)求△ABC面积的最大值．

Answer 1

【答案】（1）60°；（2）

【解析】

（1）连接BO并延长交⊙O于点D，连接CD，得到∠DCB＝90°，BD＝4，再解直角三角形即可解答.

（2）因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A应落在优弧BC的中点处，过OE⊥BC于点E，延长EO交 O于点A，则A为优弧BC的中点，连接AB，AC，则AB=AC，由圆周角定理可求出∠BAE的度数，在Rt△ABE中，利用锐角三角函数的定义及特殊角的三角函数值可求出AE的长，由三角形的面积公式即可解答．

(1)连接BO并延长交⊙O于点D，连接CD．

∵ BD是直径，∴ BD＝4，∠DCB＝90°．

在Rt△DBC中，，

∴ ∠BDC＝60°，∴ ∠BAC＝∠BDC＝60°．

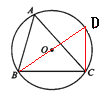
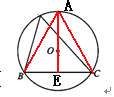
(2)因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A应落在优弧BC的中点处．

过O作OE⊥BC于点E，延长EO交⊙O于点A，则A为优孤BC的中点．连结AB，AC，

则AB＝AC，∠BAE∠BAC＝30°．

在Rt△ABE中，

∵ BE，∠BAE＝30°，

∴ ，

∴ ．

答：△ABC面积的最大值是．