ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЁЂBEFGОљЮЊе§ЗНаЮЃЎ
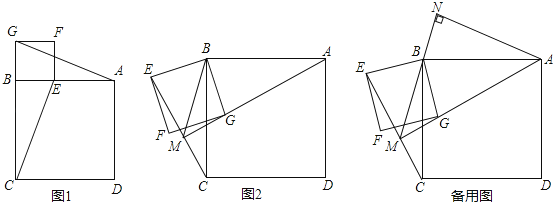
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгAGЁЂCEЃЌЪдХаЖЯAGКЭCEЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЮЊЁЁ ЁЁЃЈжБНгаДНсЙћЃЉ
ЃЈ2ЃЉНЋе§ЗНаЮBEFGШЦЕуBЫГЪБеыа§зЊІТНЧЃЈ0ЁуЃМІТЃМ180ЁуЃЉЃЌШчЭМ2ЃЌСЌНгAGЁЂCEЯрНЛгкЕуMЃЌСЌНгMBЃЌЕБНЧІТЗЂЩњБфЛЏЪБЃЌAGКЭCEЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЪЧЗёЗЂЩњБфЛЏЃПЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчБИгУЭМЃЌСЌНгMBЃЌЙ§ЕуAзїANЁЭMBНЛMBЕФбгГЄЯпгкЕуNЃЌШєMBЃН3![]() ЃЌе§ЗНаЮABCDЕФБпГЄЮЊ3
ЃЌе§ЗНаЮABCDЕФБпГЄЮЊ3![]() ЃЌЧѓBNЕФГЄЃЎ
ЃЌЧѓBNЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉAGЃНECЃЌAGЁЭECЃЛЃЈ2ЃЉНсТлВЛБфЃЌМћНтЮіЃЛЃЈ3ЃЉBNЃН![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉAG=ECЃЌAGЁЭECЃЌРэгЩЮЊЃКгЩе§ЗНаЮBEFGгые§ЗНаЮABCDЃЌРћгУе§ЗНаЮЕФаджЪЕУЕНСНЖдБпЯрЕШЃЌвЛЖджБНЧЯрЕШЃЌРћгУSASЕУГіШ§НЧаЮABGгыШ§НЧаЮCBEШЋЕШЃЌРћгУШЋЕШШ§НЧаЮЕФЖдгІБпЯрЕШЃЌЖдгІНЧЯрЕШЕУЕНCE=AGЃЌЁЯBCE=ЁЯBAGЃЌдйРћгУЭЌНЧЕФгрНЧЯрЕШМДПЩЕУжЄЃЛ
ЃЈ2ЃЉНсТлВЛБфЃЌРэгЩЮЊЃКРћгУSASЕУГіШ§НЧаЮABGгыШ§НЧаЮBECШЋЕШМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЙ§BзїBPЁЭECЃЌBHЁЭAMЃЌЪзЯШжЄУїBMЦНЗжЁЯBMEЃЌдйжЄУїCM=![]() BNЃЌЧѓГіMCМДПЩНтОіЮЪЬтЃЛ
BNЃЌЧѓГіMCМДПЩНтОіЮЪЬтЃЛ
НтЃКЃЈ1ЃЉAG=ECЃЌAGЁЭECЃЌ
РэгЩЮЊЃКШчЭМ1жаЃЌ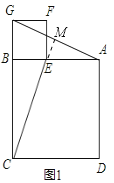
Ёпе§ЗНаЮBEFGЃЌе§ЗНаЮABCDЃЌ
ЁрGB=BEЃЌЁЯABG=90ЁуЃЌAB=BCЃЌЁЯABC=90ЁуЃЌ
дкЁїABGКЭЁїBECжаЃЌ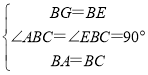 ЃЌ
ЃЌ
ЁрЁїABGЁеЁїBECЃЈSASЃЉЃЌ
ЁрCE=AGЃЌЁЯBCE=ЁЯBAGЃЌ
бгГЄCEНЛAGгкЕуMЃЌ
ЁрЁЯBEC=ЁЯAEMЃЌ
ЁрЁЯABC=ЁЯAME=90ЁуЃЌ
ЁрAG=ECЃЌAGЁЭECЃЛ
ЙЪД№АИЮЊAG=ECЃЌAGЁЭECЃЌ
ЃЈ2ЃЉНсТлВЛБфЃЎ
РэгЩЮЊЃКШчЭМ2жаЃЌЩшAMНЛBCгкOЃЎ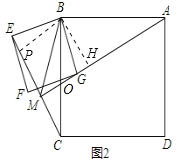
ЁпЁЯEBG=ЁЯABC=90ЁуЃЌ
ЁрЁЯABG=ЁЯEBCЃЌ
дкЁїABGКЭЁїCEBжаЃЌ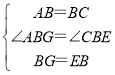 ,
,
ЃЌ
ЁрЁїABGЁеЁїCEBЃЈSASЃЉЃЌ
ЁрAG=ECЃЌЁЯBAG=ЁЯBCEЃЌ
ЁпЁЯBAG+ЁЯAOB=90ЁуЃЌЁЯAOB=ЁЯCOMЃЌ
ЁрЁЯBCE+ЁЯCOM=90ЁуЃЌ
ЁрЁЯOMC=90ЁуЃЌ
ЁрAGЁЭECЃЎ
ЃЈ3ЃЉШчЭМ2жаЃЌЙ§BзїBPЁЭECЃЌBHЁЭAMЃЌ
ЁрSЁїABG=SЁїEBCЃЌAG=ECЃЌ
Ёр
![]() ECBP=
ECBP=![]() AGBHЃЌ
AGBHЃЌ
ЁрBP=BHЃЌ
ЁрMBЮЊЁЯEMGЕФЦНЗжЯпЃЌ
ЁпЁЯAMC=ЁЯABC=90ЁуЃЌ
ЁрЁЯEMB=![]() ЁЯEMG=
ЁЯEMG=![]() ЁС90Ёу=45ЁуЃЛ
ЁС90Ёу=45ЁуЃЛ
ШчЭМ3жаЃЌдкNAЩЯНиШЁNQ=NBЃЌСЌНгBQЃЌзїBHЁЭAMгкHЃЌСЌНгACЃЎ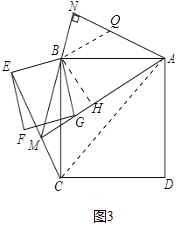
ЁрЁїBNQЮЊЕШбќжБНЧШ§НЧаЮЃЌМДBQ=![]() BNЃЌ
BNЃЌ
ЁпЁЯAMN=45ЁуЃЌЁЯN=90ЁуЃЌ
ЁрЁїAMNЮЊЕШбќжБНЧШ§НЧаЮЃЌМДAN=MNЃЌ
ЁрMN-BN=AN-NQЃЌМДAQ=BMЃЌ
ЁпЁЯMBC+ЁЯABN=90ЁуЃЌЁЯBAN+ЁЯABN=90ЁуЃЌ
ЁрЁЯMBC=ЁЯBANЃЌ
дкЁїABQКЭЁїBCMжаЃЌ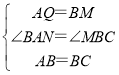 ЃЌ
ЃЌ
ЁрЁїABQЁеЁїBCMЃЈSASЃЉЃЌ
ЁрCM=BQЃЌ
дђCM=![]() BNЃЌ
BNЃЌ
ЁпЁЯBMH=45ЁуЃЌBHЁЭAMЃЌBM=3![]()
ЁрBH=HM=3ЃЌ
ЁрAH=![]() =6ЃЌ
=6ЃЌ
ЁрAM=9ЃЌAC=3![]() ЃЌ
ЃЌ
ЁрCM=![]() =3ЃЌ
=3ЃЌ
ЁрBN=![]() CM=
CM=![]() .
.

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПФГЦЗХЦЪжЛњШЅФъУПЬЈЕФЪлМлyЃЈдЊЃЉгыдТЗнxжЎМфТњзуКЏЪ§ЙиЯЕЃКyЃНЉ50x+2600ЃЌШЅФъЕФдТЯњСПpЃЈЭђЬЈЃЉгыдТЗнxжЎМфГЩвЛДЮКЏЪ§ЙиЯЕЃЌЦфжа1Љ6дТЗнЕФЯњЪлЧщПіШчЯТБэЃК
дТЗнЃЈxЃЉ | 1дТ | 2дТ | 3дТ | 4дТ | 5дТ | 6дТ |
ЯњЪлСПЃЈpЃЉ | 3.9ЭђЬЈ | 4.0ЭђЬЈ | 4.1ЭђЬЈ | 4.2ЭђЬЈ | 4.3ЭђЬЈ | 4.4ЭђЬЈ |
ЃЈ1ЃЉЧѓpЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓИУЦЗХЦЪжЛњдкШЅФъФФИідТЕФЯњЪлН№ЖюзюДѓЃПзюДѓЪЧЖрЩйЭђдЊЃП
ЃЈ3ЃЉНёФъ1дТЗнИУЦЗХЦЪжЛњЕФЪлМлБШШЅФъ12дТЗнЯТНЕСЫm%ЃЌЖјЯњЪлСПвВБШШЅФъ12дТЗнЯТНЕСЫ1.5m%ЃЎНёФъ2дТЗнЃЌОЯњЩЬОіЖЈЖдИУЪжЛњвд1дТЗнМлИёЕФЁААЫелЁБЯњЪлЃЌетбљ2дТЗнЕФЯњЪлСПБШНёФъ1дТЗндіМгСЫ1.5ЭђЬЈЃЎШєНёФъ2дТЗнетжжЦЗХЦЪжЛњЕФЯњЪлЖюЮЊ6400ЭђдЊЃЌЧѓmЕФжЕЃЎ