题目内容
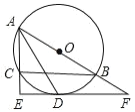
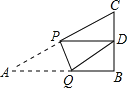
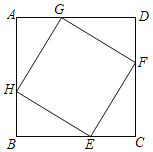
【题目】如图,点E,F,G,H分别位于边长为a的正方形ABCD的四条边上,四边形EFGH也是正方形,AG=x,正方形EFGH的面积为y.
(1)当a=2,y=3时,求x的值;
(2)当x为何值时,y的值最小?最小值是多少?
【答案】(1)x=![]() ;(2)当x=
;(2)当x=![]() a(即E在AB边上的中点)时,正方形EFGH的面积最小,最小的面积为
a(即E在AB边上的中点)时,正方形EFGH的面积最小,最小的面积为![]() a2.
a2.
【解析】
(1)设正方形ABCD的边长为a,AE=x,则BE=a﹣x,易证△AHE≌△BEF≌△CFG≌△DHG,再利用勾股定理求出EF的长,进而得到正方形EFGH的面积;
(2)利用二次函数的性质即可求出面积的最小值.
解:设正方形ABCD的边长为a,AE=x,则BE=a﹣x,
∵四边形EFGH是正方形,
∴EH=EF,∠HEF=90°,
∴∠AEH+∠BEF=90°,
∵∠AEH+∠AHE=90°,
∴∠AHE=∠BEF,
在△AHE和△BEF中, ,
,
∴△AHE≌△BEF(AAS),
同理可证△AHE≌△BEF≌△CFG≌△DHG,
∴AE=BF=CG=DH=x,AH=BE=CF=DG=a﹣x
∴EF2=BE2+BF2=(a﹣x)2+x2=2x2﹣2ax+a2,
∴正方形EFGH的面积y=EF2=2x2﹣2ax+a2,
当a=2,y=3时,2x2﹣4x+4=3,
解得:x=![]() ;
;
(2)∵y=2x2﹣2ax+a2=2(x﹣![]() a)2+
a)2+![]() a2,
a2,
即:当x=![]() a(即E在AB边上的中点)时,正方形EFGH的面积最小,最小的面积为
a(即E在AB边上的中点)时,正方形EFGH的面积最小,最小的面积为![]() a2.
a2.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
(1)这组数据的众数是多少,中位数是多少.
(2)已知获得2018年四川省南充市的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.