题目内容
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1 . 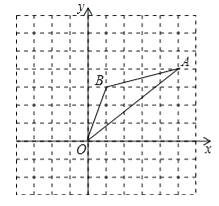
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
【答案】
(1)解:△A1OB1如图所示
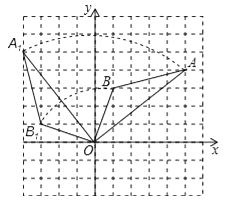
(2)![]()
(3)解: 由勾股定理得,OA= ![]() =
= ![]() ,∵AB所扫过的面积=S扇形A1OA+S△A1B1O﹣S扇形B1OB﹣S△AOB=S扇形A1OA﹣S扇形B1OB,BO扫过的面积=S扇形B1OB,∴线段AB、BO扫过的图形的面积之和=S扇形A1OA﹣S扇形B1OB+S扇形B1OB=S扇形A1OA=
,∵AB所扫过的面积=S扇形A1OA+S△A1B1O﹣S扇形B1OB﹣S△AOB=S扇形A1OA﹣S扇形B1OB,BO扫过的面积=S扇形B1OB,∴线段AB、BO扫过的图形的面积之和=S扇形A1OA﹣S扇形B1OB+S扇形B1OB=S扇形A1OA= ![]() =
= ![]()
【解析】(2)由勾股定理得,BO= ![]() =
= ![]() ,
,
所以,点B所经过的路径长= ![]() =
= ![]() ;
;
故答案为: ![]() .
.
(1)根据题意是将△AOB绕点O逆时针旋转90°后得到△A1OB1,按要求画出图形即可。
(2)根据题意可知,在旋转过程中点B所经过的路径长是以O为圆心,OB为半径,圆心角为90°的弧长,因此先利用勾股定理求出半径OB的长,再根据弧长公式求出点B所经过的路径长即可。
(3)先利用勾股定理求出OA的长,再根据图形分别表示出AB所扫过的面积和BO扫过的面积,再求和,即线段AB、BO扫过的图形的面积之和S扇形A1OA然后根据三角形的面积公式和扇形的面积公式计算即可。

【题目】在硬地上抛掷一枚图钉,通常会出现两种情况:

下面是小明和同学做“抛掷图钉实验”获得的数据:
抛掷次数n | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
针尖不着地的频数m | 63 | 120 | 186 | 252 | 310 | 360 | 434 | 488 | 549 | 610 |
针尖不着地的频率 | 0.63 | 0.60 | 0.63 | 0.60 | 0.62 | 0.61 |
(1)填写表中的空格;
(2)画出该实验中,抛掷图钉钉尖不着地频率的折线统计图;

(3)根据“抛掷图钉实验”的结果,估计“钉尖着地”的概率为 .
【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
x单位:台) | 10 | 20 | 30 |
y(单位:万元/台) | 60 | 55 | 50 |
(1)求y与x之间的函数关系式;
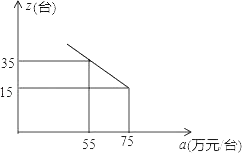
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.
①该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
②若该厂每月生产的这种机器当月全部售出,则每个月生产多少台这种机器才能使每台机器的利润最大?