题目内容
【题目】如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线y= ![]() x+
x+ ![]() 与x轴,y轴分别相交于点D,点E,连接AC并延长与y轴相交于点B,点B的坐标为(0,
与x轴,y轴分别相交于点D,点E,连接AC并延长与y轴相交于点B,点B的坐标为(0, ![]() ).
).
(1)求证:OE=CE;
(2)请判断直线CD与⊙P位置关系,证明你的结论,并求出⊙P半径的值.
【答案】
(1)证明:如图所示,连接OC,

∵直线y= ![]() x+
x+ ![]() 与y轴相交于点E,
与y轴相交于点E,
∴点E的坐标为(0, ![]() ),即OE=
),即OE= ![]() .
.
又∵点B的坐标为(0, ![]() ),
),
∴OB= ![]() ,
,
∴BE=OE= ![]() ,
,
又∵OA是⊙P的直径,
∴∠ACO=90°,即OC⊥AB,
∴OE=CE.
(2)直线CD是⊙P的切线.
证明:连接PC,PE,由(1)可知OE=CE.
在△POE和△PCE中, 
∴△POE≌△PCE,
∴∠POE=∠PCE.
又∵x轴⊥y轴,
∴∠POE=∠PCE=90°,
∴PC⊥CE,即PC⊥CD.
又∵直线CD经过半径PC的外端点C,
∴直线CD是⊙P的切线.
∵对y= ![]() x+
x+ ![]() ,当y=0时,x=-6,即OD=6,
,当y=0时,x=-6,即OD=6,
在Rt△DOE中,DE= ![]() =
= ![]() =
= ![]() ,
,
∴CD=DE+EC=DE+OE= ![]() +
+ ![]() =
= ![]() .
.
设⊙P的半径为r,
则在Rt△PCD中,由勾股定理知PC2+CD2=PD2,
即r2+(6 ![]() )2=(6+r)2,
)2=(6+r)2,
解得r=6,即⊙P半径的值为6.
【解析】(1)连接OC,利用已知条件计算出CE和OB的长度,再证明△BCO为直角三角形,利用:直角三角形斜边上的中线等于斜边的一半即可证明OE=CE。
(2)①要证直线CD是⊙P的切线,需证明PC⊥CD,先证明△POE≌△PCE,得出∠POE=∠PCE,再根据∠POE是直角,证明PC⊥CD即可得出结论;
②设⊙P的半径为r,则在Rt△PCD中,由勾股定理得到关于r的方程,求出r即可。

【题目】在硬地上抛掷一枚图钉,通常会出现两种情况:

下面是小明和同学做“抛掷图钉实验”获得的数据:
抛掷次数n | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
针尖不着地的频数m | 63 | 120 | 186 | 252 | 310 | 360 | 434 | 488 | 549 | 610 |
针尖不着地的频率 | 0.63 | 0.60 | 0.63 | 0.60 | 0.62 | 0.61 |
(1)填写表中的空格;
(2)画出该实验中,抛掷图钉钉尖不着地频率的折线统计图;

(3)根据“抛掷图钉实验”的结果,估计“钉尖着地”的概率为 .
【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
x单位:台) | 10 | 20 | 30 |
y(单位:万元/台) | 60 | 55 | 50 |
(1)求y与x之间的函数关系式;
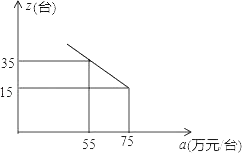
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.
①该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
②若该厂每月生产的这种机器当月全部售出,则每个月生产多少台这种机器才能使每台机器的利润最大?