题目内容
 如图在△ABC中,∠ABC和∠ACB的平分线相交于D,过D作EF∥BC,交AB于E,交AC于F.
如图在△ABC中,∠ABC和∠ACB的平分线相交于D,过D作EF∥BC,交AB于E,交AC于F.
(1)图中共有多少个等腰三角形?是那几个?
(2)EF与BE、CF之间有何关系?请说明你的结论的正确性.
解:(1)共有2个等腰三角形,是△DEB和△DFC.
理由是:∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴DE=BE,CF=DF,
即△DEB和△DFC是等腰三角形.
(2)EF与BE、CF之间的关系是EF=BE+CF.
理由是:由(1)知BE=DE,CF=DF,
∴EF=DE+DF=BE+CF,
即EF=BE+CF.
分析:(1)根据平行线性质和角平分线性质求出∠EDB=∠EBD,∠FDC=∠FCD,推出DE=BE,CF=DF即可;
(2)根据DE=BE,CF=DF,代入EF=DE+DF,即可求出答案.
点评:本题考查了等腰三角形的性质和判定,平行线的性质,角平分线定义等知识点的应用,能推出BE=DE和CF=DF是解此题的关键,题目比较典型,难度也不大.
理由是:∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴DE=BE,CF=DF,
即△DEB和△DFC是等腰三角形.
(2)EF与BE、CF之间的关系是EF=BE+CF.
理由是:由(1)知BE=DE,CF=DF,
∴EF=DE+DF=BE+CF,
即EF=BE+CF.
分析:(1)根据平行线性质和角平分线性质求出∠EDB=∠EBD,∠FDC=∠FCD,推出DE=BE,CF=DF即可;
(2)根据DE=BE,CF=DF,代入EF=DE+DF,即可求出答案.
点评:本题考查了等腰三角形的性质和判定,平行线的性质,角平分线定义等知识点的应用,能推出BE=DE和CF=DF是解此题的关键,题目比较典型,难度也不大.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,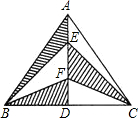 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是