题目内容
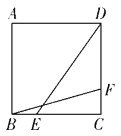
【题目】如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
连接AE,利用△ABE≌△BCF转化线段BF得到BF+DE=AE+DE,则通过作A点关于BC对称点H,连接DH交BC于E点,利用勾股定理求出DH长即可.
解:解:连接AE,如图1,
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°.
又BE=CF,
∴△ABE≌△BCF(SAS).
∴AE=BF.
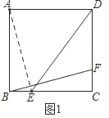
所以BF+DE最小值等于AE+DE最小值.
作点A关于BC的对称点H点,如图2,
连接BH,则A、B、H三点共线,
连接DH,DH与BC的交点即为所求的E点.
根据对称性可知AE=HE,
所以AE+DE=DH.
在Rt△ADH中,DH2=AH2+AD2=82+42=80
∴DH=4![]()
∴BF+DE最小值为4![]()
故选: D.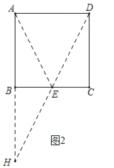

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
已知某中学计划租用A、B两种型号的客车共10辆,同时送七年级师生到沙家参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆A型号客车?
(2)若七年级的师生共有380人,请写出所有可能的租车方案.




