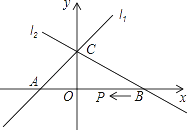
题目内容
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转![]() °(0°<
°(0°<![]() <180°),分别交直线BC、AD于点E、F.
<180°),分别交直线BC、AD于点E、F.

(1)当![]() =_____°时,四边形ABEF是平行四边形;
=_____°时,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形,
①当![]() =_______°时,构造的四边形是菱形;
=_______°时,构造的四边形是菱形;
②若构造的四边形是矩形,求该矩形的两边长.
【答案】(1)90;(2)①45或90;②![]() 和
和![]() ;
;![]() 和
和![]()
【解析】
(1)根据平行四边形的判断方法即可解决问题;
(2)①分两种情形分别解决问题即可;
②分两种情形讨论求解即可;
解:(1)当α=90°,四边形ABEF是平行四边形;
理由:∵AB⊥AC,
∴∠BAO=∠AOF=90°,
∴AB∥EF,
∵平行四边形ABCD
∴AF∥BE,
∴四边形ABEF是平行四边形.
故答案为:90°.
(2)①当α=45°或90°时,四边形BEDF是菱形.
当α=45°时
∵AD∥BC,
∴∠FDO=∠EBO,
∵∠FOD=∠BOE,OD=OB,
∴△FDO≌△EBO,
∴DF=BE,
∵DF∥BE,
∴四边形BEDF是平行四边形,
∵OA=OC=2,AB=2,
∴AB=OA,
∴∠AOB=45°,
∴∠BOF=45°+45°=90°,
∴BD⊥EF,
∴四边形BEDF是菱形.
当α=90°时,同法可证四边形AFCE是菱形.
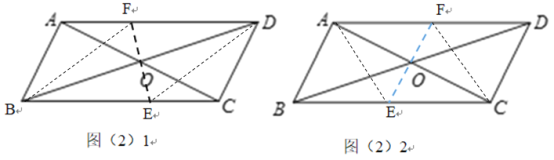
故答案为:45°或90°.
②∵AB⊥AC,AB=2,AC=4,
∴BC=2![]() ,
,
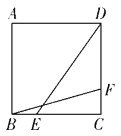
当EF=AC时,四边形AECF是矩形,对角线AC=4,过A点作AE⊥BC于BC,过点C作CF⊥AD于F,如图1,
∴△AEB∽△BAC
∴![]()
∴AE2+BE2=AB2
∴BE=![]() ,AE=
,AE=![]()
∴EC=BC-BE=![]()
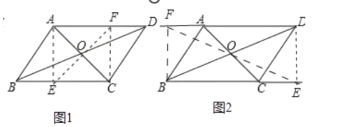
过B作BF⊥AD于F,过D作DE⊥BC于E,
此时四边形BEDF是矩形,EF=BD,如图2
同理可得:DA=BC=2![]() ,AF=
,AF=![]() ,BF =
,BF =![]() ,
,
∴BE=DF=DA+FA=![]()
矩形的边长为:![]() 和
和![]() 或
或![]() 和
和![]()
故答案为:![]() 和
和![]() 或
或![]() 和
和![]()