��Ŀ����
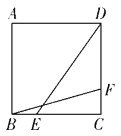
����Ŀ����֪ABC��ƽ��ֱ������ϵ�ڣ����㣺��A��y�����������ƶ�����B��x�Ḻ�������ƶ�����CΪy���Ҳ�һ���㣮

��A0,a�͵�Bb,0����ǡ�����㣺![]() ��ֱ��д��a,b��ֵ��
��ֱ��д��a,b��ֵ��
����ͼ�٣�����C�ڵ�������ʱ����AM��AO��BAC���ȷ֣�BM��BO��ABC���ȷ֣���A��B��C���˶������У������C��M�Ĺ�ϵ��
��̽����
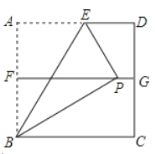
��i����ͼ�ڣ�����C�ڵ�������ʱ����AMƽ��CAO,BMƽ��CBO,��A��B��C���˶������У�C��M�Ƿ����ȷ����������ϵ�������ڣ���֤����Ľ��ۣ��������ڣ���˵�����ɣ�
��ii����ͼ�ۣ�����C�ڵ�һ����ʱ�����ڣ�i���е����������ǰ���£�C��M���к�������ϵ��֤����Ľ��ۣ�
���𰸡�(1)a=-2,b=3; (2) ��M-��C=90�㣨���M+��C=180�㣬����M���C����.������3����i��2��M-��C=90�㣻 ��ii��2��M-��C=90��.
��������
��1�����ݷǸ��������ʵõ�����a,b�Ķ�Ԫһ�η����飬�ⷽ���鼴�ɣ�
��2���������ȷ��ߵ����ʿɵó���CAB=3��MAB,��CBA=3��MBA����OAB=2��MAB,��OBA=2��MBA.���������ε��ڽǺ͵���180�㣬�������OAB+��OBA=90�����Ӷ��ó���MAB+��MBA=45������CAB+��CBA=135�����ٴθ��������ε��ڽǺ͵���180��ֱ������M=135�㣬��C=45�㣬�Ӷ��ó���M-��C=90��.
��3�����ݽ�ƽ���ߵĶ���������ε��ڽǺͶ����ɵó�����2��M-��C=90��.
�⣺��1����![]()
��![]() ,��ã�
,��ã�![]()
��a,b��ֵ�ֱ�Ϊ2��-3.
��2����ͼ1.��M-��C=90��.�������£�
��AM��AO��BAC���ȷ֣�
���CAB=3��MAB,��MAB=![]() ��OAB.
��OAB.
��BM��BO��ABC���ȷ֣�
���CBA=3��MBA,��MBA=![]() ��OBA.
��OBA.
�ߡ�OAB+��OBA=90�㣬
���MAB+��MBA=![]() 90��=45�㣬
90��=45�㣬
�ߡ�MAB+��MBA+��M=180�㣬
���M=135��.
�ߡ�MAB+��MBA=45�㣬
���CBA+��CAB=3����MAB+��MBA��=3![]() 45��=135�㣬
45��=135�㣬
�ߡ�CBA+��CAB+��C=180��.
���C=45��.
���M-��C=90��.�����M+��C=180�㣬����M���C����.��
��3����i����ͼ2.��AMƽ��CAO,
���CAO=2��MAO.
��BMƽ��CBO,
��CBO=2MBO.
���CAO+CBO=2��MAO+2MBO=2(��MAO+MBO)
�ߡ�C+��CAO+��OAB+��OBA+��CBO=180�㣬��OAB+��OBA=90�㣬
���C+��CAO+��CBO=180��-90��=90��.
���C+2(��MAO+MBO)= 90��.
�ߡ�M+��MAO+��OAB+��OBA+��MBO=180�㣬
���M+��MAO+��MBO=180��-����OAB+��OBA��=180��-90��=90��.
���MAO+��MBO=90��-��M
�ߡ�C+2(��MAO+MBO)= 90�㣬
���C+2(90��-��M) = 90��.
��2��M-��C=90��.
��ii����ͼ3. ��AMƽ��CAO,
���CAO=2��MAO.
��BMƽ��CBO,
��CBO=2MBO.
���CAO-CBO=2(��MAO-MBO)
�ߡ�C+��CAO+��0AB+��OBA-��CBO=180�㣬�ҡ�OAB+��OBA=90�㣬
���C+��CAO-��CBO=90��.
���C+2(��MAO-MBO)= =90��.
�ߡ�M+��MAO+��0AB+��OBA-��MBO=180��,
���M+��MAO-��MBO=90��,
���MAO-��MBO=90��-��M.
���C+2(90��-��M)= 90��,
��2��M-��C=90��.