题目内容
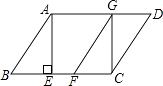
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3 ![]() ,BG=4,则GH的长为 .
,BG=4,则GH的长为 . 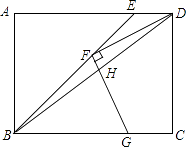
【答案】![]()
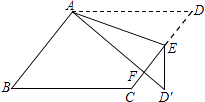
【解析】解:解法一:如右图,过点F作BC的垂线,分别交BC、AD于点M、N,则MN⊥AD,延长GF交AD于点Q,如图所示.
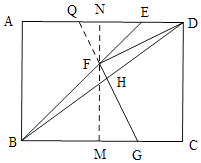
∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°,
∴△MBF是等腰直角三角形,
∵BF=3 ![]() ,
,
∴BM=FM=3,
∵BG=4,
∴MG=1,
∵FD⊥FG,
∴∠DFG=90°,
∴∠DFN+∠MFG=90°,
∵∠DNF=90°,
∴∠NDF+∠DFN=90°,
∴∠NDF=∠MFG,
在DNF和△FMG中,
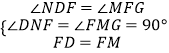 ,
,
∴△DNF≌△FMG(AAS),
∴DN=FM=3,NF=MG=1,
由勾股定理得:FG=FD= ![]() ,
,
∵QN∥BC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴FQ= ![]() ,QN=
,QN= ![]() ,
,
设GH=x,则FH= ![]() ﹣x,
﹣x,
∵QD∥BG,
∴ ![]() ,
,
∴ ![]() ,
,
x= ![]() ,
,
即GH= ![]() .
.
解法二:如右图,过F作FN⊥BC于N,过B作BM⊥FG于M,
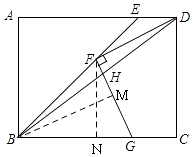
∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°,
∴△NBF是等腰直角三角形,
∵BF=3 ![]() ,
,
∴BN=FN=3,
∵BG=4,
∴NG=1,
在Rt△FNG中,由勾股定理得:DF=FG= ![]() =
= ![]() ,
,
∵S△BFG= ![]() BGFN=
BGFN= ![]() FGBM,
FGBM,
∴4×3= ![]() BM,
BM,
∴BM= ![]() ,
,
∴GM= ![]() =
= ![]() =
= ![]() ,
,
∴FM=GF﹣GM= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∵DF∥BM,
∴△DFH∽△BMH,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴HM= ![]() ,
,
∴GH=HM+GM= ![]() +
+ ![]() =
= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】本题主要考查了三角形的面积和矩形的性质的相关知识点,需要掌握三角形的面积=1/2×底×高;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.