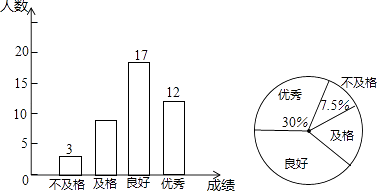
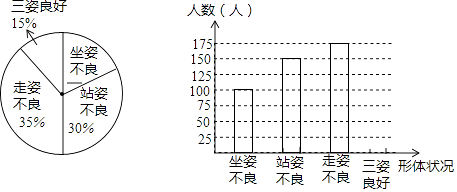
题目内容
【题目】已知:如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.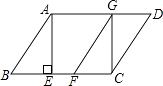
(1)求证:BE=DG;
(2)已知tanB= ![]() ,AB=5,若四边形ABFG是菱形,求平行四边形ABCD的面积.
,AB=5,若四边形ABFG是菱形,求平行四边形ABCD的面积.
【答案】
(1)解:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∵AE⊥BC,CG∥AE,
∴CG⊥AD,
∴∠AEB=∠CGD=90°,AE=CG,
在Rt△ABE和Rt△CDG中,
![]() ,
,
∴Rt△ABE≌Rt△CDG,
∴BE=DG.
(2)解:∵tanB= ![]() =
= ![]() ,设AE=4k,BE=3k,
,设AE=4k,BE=3k,
∵AB2=AE2+BE2,
∴52=(3k)2+(4k)2,
∴k=1,
∴AE=4,BE=3,
∵四边形ABFG是菱形,
∴AG=AB=5,
∵四边形AGCE是矩形,
∴AG=EC=5,
∴BC=3+5=8,
∴S平行四边形ABCD=BCAE=32.
【解析】根据平移的性质得出CG⊥AD、AE=CG,根据直角三角形全等判定方法,证明Rt△ABE≌Rt△CDG,即可求证结论。
(2)根据tanB及AB的值,在Rt△ABE中,根据勾股定理及解直角三角形,易求得AE、BE的长,由四边形ABFG是菱形,求出AG的值,四边形AGCE是矩形,求出EC、BC的值,即可求出平行四边形ABCD的面积。
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】网络商店(简称网店)是近年来迅速兴起的一种电子商务形式,小明的网店销售红枣、小米两种商品的相关信息如下表:
商品 | 红枣 | 小米 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 40 | 38 |
售价(元/袋) | 60 | 54 |
根据上表提供的信息,解答下列问题
(1)已知今年前四个月,小明的网店销售上表中规格的红枣和小米共2000kg,获得利润2.8万元,求这前四个月小明的网店销售这种规格的红枣和小米各多少袋?
(2)根据之前的销售情况,估计今年5月到12月这后八个月,小明的网店还能销售同规格的红枣和小米共4000kg,其中,红枣的销售量不低于1200kg.假设这后八个月,销售红枣x(kg),销售红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后八个月,小明的网店销售这种规格的红枣和小米至少获得总利润多少元?