Question

【题目】在平面直角坐标系中，二次函数的图像经过点M（，n），点N（，n），交y轴于点A．

（1）求a，b满足的关系式；

（2）若抛物线上始终存在不重合的P，Q两点（P在Q的左边）关于原点对称．

①求a的取值范围；

②若点A，P，Q三点到直线l:的距离相等，求线段PQ长．

Answer 1

【答案】（1）；（2）①,②

【解析】

（1）根据M、N的坐标确定二次函数图像的对称轴=，然后用a表示b即可；

（2）①设，则，将P，Q两点代入表达式得到并求解即可确定a的取值范围内；②先说明B为OA中点，再分别作PD⊥l于D点，QE⊥l于E点；然后就P、Q在直线l异侧和同侧两种情况解答即可．

解：（1）∵函数图像经过点M（，n），点N（，n）

则该函数的对称轴为直线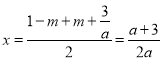

∴

∴；

（2）①设，则，将P，Q两点代入表达式有：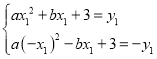

由①+②得：③

∵始终存在，故方程③始终有解，

∴，可得：

②∵，则A点坐标为（0，3），

∵设直线交y轴于点B，则B点坐标为

∴B为OA中点．

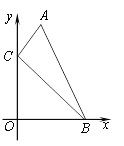
分别作PD⊥l/span>于D点，QE⊥l于E点．

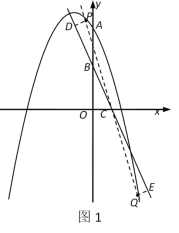
若P，Q位于直线l异侧，如图1，连接PQ，交直线l于C点．

由已知得PD=QE，

又∵∠PDC=∠QEC=90°，∠PCD=∠QCE，

∴△PDC≌△QEC

∴CP=CQ

∴C为PQ的中点，

∵O为PQ中点，但直线l并没有经过点O，

∴不存在这种情况．

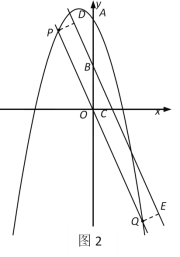
若P，Q位于直线l同侧，由PD=QE得PQ∥l．

又∵PQ经过原点O，

∴直线PQ的表达式为：．

∴．

由①知道：

则有：

解得：．

∵

∴．

解得：．

∴．

∴．

∴．

∴．

∴．

∴．