题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°
(1)请用尺规作图法,作∠ACB的平分线CD,交AB于点D;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,过点D分别作DE![]() AC于点E,DF
AC于点E,DF![]() BC于点F,四边形CEDF_____形
BC于点F,四边形CEDF_____形
【答案】(1)见解析;(2)正方形
【解析】
(1)依据角平分线的尺规作图方法进行作图即可;
(2)要证四边形CEDF是正方形,则要先证明四边形DECF是矩形,已知CD平分∠ACB,DE⊥AC,DF⊥BC,故可根据有三个角是直角的四边形是矩形判定,再根据正方形的判定方法得到四边形CEDF是正方形.
解:(1)如图所示,CD即为所求;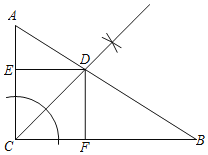
(2)证明:∵CD平分∠ACB,DE⊥AC,DF⊥BC,
∴DE=DF,∠DFC=90°,∠DEC=90°,
又∵∠ACB=90°,
∴四边形DECF是矩形,
∵DE=DF,
∴矩形DECF是正方形.

 优加精卷系列答案
优加精卷系列答案【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:
速度v(千米/小时) | …… | 5 | 10 | 20 | 32 | 40 | 48 | …… |
流量q(辆/小时) | …… | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | …… |
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是___________.(只填上正确答案的序号)
①q=90v+100;②q=![]() ;③q=2v2+120v.
;③q=2v2+120v.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当18≤v≤28该路段不会出现交通拥堵现象.试分析当车流密度k在什么范围时,该路段不会出现交通拥堵现象;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,当d=25米时请求出此时的速度v.