题目内容
【题目】在△ABC中,∠C=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至G,使CG=BF,连接CE、DE、DG.

(1)如图1,求证:四边形CEDG是平行四边形;
(2)如图2,连接EG交AC于点H,若EG⊥AB,请直接写出图2中所有长度等于![]() GH的线段.
GH的线段.
【答案】(1)见解析;(2)AE、EB、EC、GD;
【解析】
(1)欲证明四边形CEDG是平行四边形,只要证明DE∥CG,DE=CG即可.
(2)由四边形四边形CEDG是平行四边形,推出DH=CH,GH=HE,设DH=CH=a,则AD=CD=2a,由∠A=∠A,∠AEH=∠ADE=90°,推出△ADE∽△AEH,推出AE2=ADAH=2a3a=6a2,推出AE=![]() a,在Rt△AEH中,HE=
a,在Rt△AEH中,HE=
![]() =
=![]() a,推出AE=
a,推出AE=![]() HE,因为GH=HE,AE=EB=CE=CD,即可推出线段AE、EB、EC、GD都是线段GH的
HE,因为GH=HE,AE=EB=CE=CD,即可推出线段AE、EB、EC、GD都是线段GH的![]() 倍.
倍.
(1)证明:如图1中,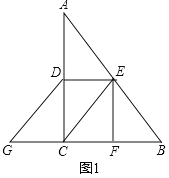
∵∠ACB=90°,AE=EB,
∴EC=EA=EB,
∵EF⊥BC,
∴CF=FB,
∵AD=DC,AE=EB,
∴DE∥BC,DE=![]() BC=BF,
BC=BF,
∵CG=BF,
∴DE=CG,DE∥CG,
∴四边形CEDG是平行四边形;
(2)解:如图2中,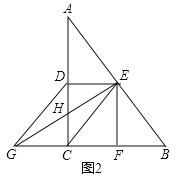
∵四边形四边形CEDG是平行四边形,
∴DH=CH,GH=HE,设DH=CH=a,则AD=CD=2a,
∵∠A=∠A,∠AEH=∠ADE=90°,
∴△ADE∽△AEH,
∴AE2=ADAH=2a3a=6a2,
∴AE=![]() a,
a,
在Rt△AEH中,HE=
![]() =
=![]() a,
a,
∴AE=![]() HE,
HE,
∵GH=HE,AE=EB=CE=GD,
∴线段AE、EB、EC、GD都是线段GH的![]() 倍.
倍.

 53随堂测系列答案
53随堂测系列答案【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间 | 频数 | 频率 |
A |
| 6 |
|
B |
| a |
|
C |
| 10 |
|
D |
| 8 | b |
E |
| 4 |
|
合计 | 1 |
请根据图表中的信息,解答下列问题:
![]() 表中的
表中的![]() ______,
______,![]() ______,中位数落在______组,将频数分布直方图补全;
______,中位数落在______组,将频数分布直方图补全;
![]() 估计该校2000名学生中,每周课余阅读时间不足
估计该校2000名学生中,每周课余阅读时间不足![]() 小时的学生大约有多少名?
小时的学生大约有多少名?
![]() 组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.
组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.




