题目内容
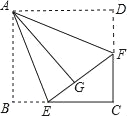
【题目】如图,已知菱形ABCD的边长为2,∠DAB=60°,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.连接BD.
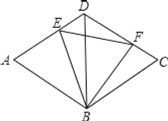
(1)图中有几对三角形全等?试选取一对全等的三角形给予证明;
(2)判断△BEF的形状,并说明理由.
(3)当△BEF的面积取得最小值时,试判断此时EF与BD的位置关系.
【答案】(1)△BAE≌△BDF,△BDE≌△BCF,△BAD≌△BCD,共三对;证明见解析;(2)△BEF为正三角形.理由见解析;(3)此时BD垂直平分EF.
【解析】
(1)可根据题意判断出△BAD≌△BCD(SSS)
△BAE≌△BD(SAS)△BDE≌△BCF(SAS),任选一组证明即可.
(2)首先由(1)知△BDE≌△BCF,得到BE=BF,再根据∠DBE=∠CB,∠DBC=∠DBF+∠CBF=60,得到一个角为60°即可证明为等边三角形.
(3)设BE=BF=EF=x,由S△BEF=![]() ,即面积根x值有关,当x最小,即BE垂直于AD时面积最小.
,即面积根x值有关,当x最小,即BE垂直于AD时面积最小.
(1)△BAE≌△BDF,△BDE≌△BCF,△BAD≌△BCD,共三对;
证明:△BDE≌△BCF.
在△BDE和△BCF中,
 ,
,
故△BDE≌△BCF.
(2)△BEF为正三角形.
理由:∵△BDE≌△BCF,
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为等边三角形;
(3)设BE=BF=EF=x,
则S△BEF=![]() xxsin60°=
xxsin60°=![]() x2,
x2,
当BE⊥AD时,x最小=2×sin60°=![]() ,此时△BEF的面积最小,
,此时△BEF的面积最小,
此时点E、F分别位于AD、CD的中点,
故此时BD垂直平分EF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目