题目内容
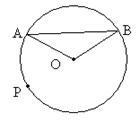
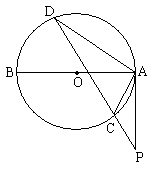
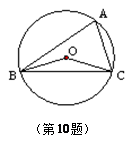
已知,如图,AB为⊙O的直径,弦DC延长线上有一点P,∠PAC=∠PDA.
小题1:求证:PA是⊙O的切线;
小题2:若AD=6,∠ACD=60°, 求⊙O的半径.
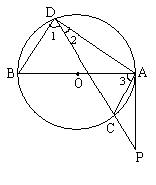
小题1:求证:PA是⊙O的切线;
小题2:若AD=6,∠ACD=60°, 求⊙O的半径.


小题1:连结BD,
∵AB是⊙O的直径,点D在⊙O上,∴∠ADB=90°.
∴∠1+∠2=90°.
∵∠1=∠3, ∠2=∠PAC,
∴∠3+∠PAC=∠1+∠2
∴∠APB=∠3+∠PAC=90°.
又OA是⊙O的半径,∴PA是⊙O的切线.
小题1:∵∠B=∠ACD=60°.
在Rt△ABD中,∠BAD=30°,AD=6.
设BD=x,AB=2x,
由AD2+BD2=AB2得 x2+62=(2x)2.
解得 x=
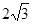 ∴⊙O的半径为
∴⊙O的半径为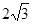 .
.要证明PA是⊙O的切线只要证明∠PAB=90°即可;已知PA是⊙O的切线,PCD是割线,则可以利用切割线定理来求得PD的长.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
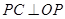 ,PC交⊙O于点C,若AP=4,PB=2,则PC的长为__◆ .
,PC交⊙O于点C,若AP=4,PB=2,则PC的长为__◆ .

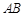 、
、 相交于点
相交于点 ,若
,若 ,
,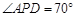 ,则
,则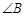 等于( )
等于( )
 ,⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S
,⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S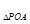 =S
=S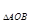 时,则点P所经过的弧长是
时,则点P所经过的弧长是