题目内容
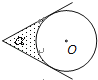
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)利用直角三角形斜边中线是斜边一半,求得DE=AE=AF=DF,
所以AEDF是菱形.
(2)由(1)得,AEDF是菱形,求得菱形对角线乘积的一半,求面积 .
试题解析:
(1)∵AD⊥BC,点E、F分别是AB、AC的中点,
∴Rt△ABD中,DE=![]() AB=AE,
AB=AE,
Rt△ACD中,DF=![]() AC=AF,
AC=AF,
又∵AB=AC,点E、F分别是AB、AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形.
(2)如图,∵菱形AEDF的周长为12,
∴AE=3,
设EF=x,AD=y,则x+y=7,
∴x2+2xy+y2=49,①
∵AD⊥EF于O,
∴Rt△AOE中,AO2+EO2=AE2,
∴(![]() y)2+(
y)2+(![]() x)2=32,
x)2=32,
即x2+y2=36,②
把②代入①,可得2xy=13,
∴xy=![]() ,
,
∴菱形AEDF的面积S=![]() xy=
xy=![]() .
.


练习册系列答案
相关题目