Question

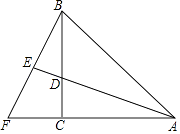
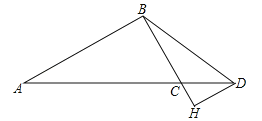
【题目】如图，在△ABC中，∠ABC=90°，BC=3，D为AC延长线上一点，AC=3CD，过点D作DH∥AB，交BC的延长线于点H．

（1）求BDcos∠HBD的值；

（2）若∠CBD=∠A，求AB的长．

Answer 1

【答案】（1）4；（2）6．

【解析】

试题分析：（1）首先根据DH∥AB，判断出△ABC∽△DHC，即可判断出=3；然后求出BH的值是多少，再根据在Rt△BHD中，cos∠HBD=，求出BDcos∠HBD的值是多少即可；

（2）首先判断出△ABC∽△BHD，推得；然后根据△ABC∽△DHC，推得，所以AB=3DH；最后根据，求出DH的值是多少，进而求出AB的值是多少即可．

试题解析：（1）∵DH∥AB，∴∠BHD=∠ABC=90°，∴△ABC∽△DHC，∴=3，∴CH=1，BH=BC+CH，在Rt△BHD中，cos∠HBD=，∴BDcos∠HBD=BH=4；

（2）∵∠CBD=∠A，∠ABC=∠BHD，∴△ABC∽△BHD，∴，∵△ABC∽△DHC，∴，∴AB=3DH，∴，解得DH=2，∴AB=3DH=3×2=6，即AB的长是6．