题目内容
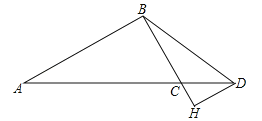
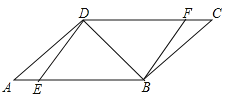
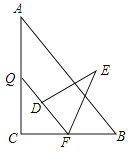
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
【答案】(1)证明见试题解析;(2)6;(3)1≤x≤![]() .
.
【解析】
试题分析:(1)先由勾股定理求出AC的长,再由相似三角形的判定定理得出△PQC∽△BAC,得出∠CPQ=∠B,由此可得出结论;
(2)连接AD,由PQ∥AB可得∠ADQ=∠DAB,再由点D在∠BAC的平分线上,得到∠DAQ=∠DAB,故∠ADQ=∠DAQ,AQ=DQ.在Rt△CPQ中根据勾股定理可知,AQ=12﹣4x,故可得出x的值,进而得出结论;
(3)当点E在AB上时,根据等腰三角形的性质求出x的值,再分0<x≤![]() ;
;![]() <x<3两种情况进行分类讨论.
<x<3两种情况进行分类讨论.
试题解析:(1)∵在Rt△ABC中,AB=15,BC=9,∴AC=![]() =
=![]() =12.∵
=12.∵![]() ,
,![]() ,∴
,∴![]() .∵∠C=∠C,∴△PQC∽△BAC,∴∠CPQ=∠B,∴PQ∥AB;
.∵∠C=∠C,∴△PQC∽△BAC,∴∠CPQ=∠B,∴PQ∥AB;
(2)连接AD,∵PQ∥AB,∴∠ADQ=∠DAB,∵点D在∠BAC的平分线上,∴∠DAQ=∠DAB,∴∠ADQ=∠DAQ,∴AQ=DQ,在Rt△CPQ中,PQ=5x,∵PD=PC=3x,∴DQ=2x.∵AQ=12﹣4x,∴12﹣4x=2x,解得x=2,∴CP=3x=6;
(3)当点E在AB上时,∵PQ∥AB,∴∠DPE=∠PEB.∵∠CPQ=∠DPE,∠CPQ=∠B,∴∠B=∠PEB,∴PB=PE=5x,∴3x+5x=9,解得x=![]() .
.
①当0<x≤![]() 时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤
时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤![]() ;
;
②当![]() <x<3时,设PE交AB于点G,DE交AB于F,作GH⊥FQ,垂足为H,∴HG=DF,FG=DH,Rt△PHG∽Rt△PDE,∴
<x<3时,设PE交AB于点G,DE交AB于F,作GH⊥FQ,垂足为H,∴HG=DF,FG=DH,Rt△PHG∽Rt△PDE,∴![]() ,∵PG=PB=9﹣3x,∴
,∵PG=PB=9﹣3x,∴![]() ,∴GH=
,∴GH=![]() (9﹣3x),PH=
(9﹣3x),PH=![]() (9﹣3x),∴FG=DH=3x﹣
(9﹣3x),∴FG=DH=3x﹣![]() (9﹣3x),∴T=PG+PD+DF+FG=(9﹣3x)+3x+
(9﹣3x),∴T=PG+PD+DF+FG=(9﹣3x)+3x+![]() (9﹣3x)+[3x﹣
(9﹣3x)+[3x﹣![]() (9﹣3x)]=
(9﹣3x)]=![]() ,此时,
,此时,![]() <T<18.∴当0<x<3时,T随x的增大而增大,∴T=12时,即12x=12,解得x=1;TA=16时,即
<T<18.∴当0<x<3时,T随x的增大而增大,∴T=12时,即12x=12,解得x=1;TA=16时,即![]() =16,解得x=
=16,解得x=![]() .∵12≤T≤16,∴x的取值范围是1≤x≤
.∵12≤T≤16,∴x的取值范围是1≤x≤![]() .
.


【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):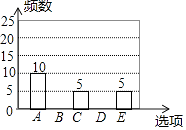
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图;
(3)若该中学约有2400名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.