题目内容
【题目】问题呈现：
（Ⅰ）如图1，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上，AE=DG，求证：2S四边形EFGH=S矩形ABCD ． （S表示面积）
（Ⅱ）实验探究：某数学实验小组发现：若图1中AH≠BF，点G在CD上移动时，上述结论会发生变化，分别过点E、G作BC边的平行线，再分别过点F、H作AB边的平行线，四条平行线分别相交于点A1、B1、C1、D1 ， 得到矩形A1B1C1D1 ．
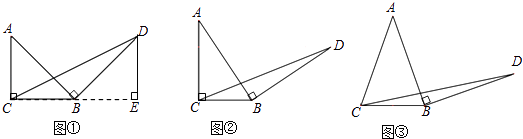
如图2，当AH＞BF时，若将点G向点C靠近（DG＞AE），经过探索，发现：2S四边形EFGH=S矩形ABCD+S 
．
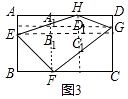
如图3，当AH＞BF时，若将点G向点D靠近（DG＜AE），请探索S四边形EFGH、S矩形ABCD与S 之间的数量关系，并说明理由．
（Ⅲ）迁移应用：
请直接应用“实验探究”中发现的结论解答下列问题：
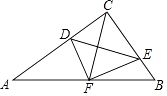
⑴如图4，点E、F、G、H分别是面积为25的正方形ABCD各边上的点，已知AH＞BF，AE＞DG，S四边形EFGH=11，HF= 
，求EG的长．
⑵如图5，在矩形ABCD中，AB=3，AD=5，点E、H分别在边AB、AD上，BE=1，DH=2，点F、G分别是边BC、CD上的动点，且FG= 
，连接EF、HG，请直接写出四边形EFGH面积的最大值．
【答案】（Ⅰ）证明：如图1中，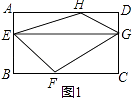
∵四边形ABCD是矩形，
∴AB∥CD，∠A=90°，
∵AE=DG，
∴四边形AEGD是矩形，
∴S△HGE= 
S矩形AEGD ，
同理S△EGF= S矩形BEGC ，
∴S四边形EFGH=S△HGE+S△EFG= S矩形ABCD ．
（Ⅱ）实验探究：结论：2S四边形EFGH=S矩形ABCD﹣ 
．
理由：∵ 
= 
， 
= 
， 
= 
， 
= 
，
∴S四边形EFGH= + + + ﹣ ，
∴2S四边形EFGH=2 +2 +2 +2 ﹣2 ，
∴2S四边形EFGH=S矩形ABCD﹣ ．
（Ⅲ）迁移应用：解：（1）如图4中，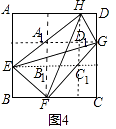
∵2S四边形EFGH=S矩形ABCD﹣ ．
∴ =25﹣2×11=3=A1B1A1D1 ，
∵正方形的面积为25，∴边长为5，
∵A1D12=HF2﹣52=29﹣25=4，
∴A1D1=2，A1B1= 
，
∴EG2=A1B12+52= 
，
∴EG= 
．
⑵解：∵2S四边形EFGH=S矩形ABCD+ ．
∴四边形A1B1C1D1面积最大时，矩形EFGH的面积最大．
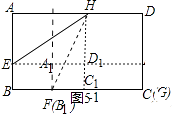
①如图5﹣1中，当G与C重合时，四边形A1B1C1D1面积最大时，矩形EFGH的面积最大．
此时矩形A1B1C1D1面积=1（ 
﹣2）= 
②如图5﹣2中，当G与D重合时，四边形A1B1C1D1面积最大时，矩形EFGH的面积最大．
此时矩形A1B1C1D1面积=21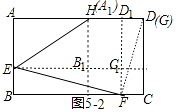=2，
∵2＞ ﹣2，
∴矩形EFGH的面积最大值= 
．
【解析】（Ⅰ）问题呈现：只要证明S△HGE= S矩形AEGD ， 同理S△EGF= S矩形BEGC ， 由此可得S四边形EFGH=S△HGE+S△EFG= S矩形BEGC；（Ⅱ）实验探究：结论：2S四边形EFGH=S矩形ABCD﹣ ．根据 = ， = ， = ， = ，即可证明；（Ⅲ）迁移应用：（1）利用探究的结论即可解决问题．（2）分两种情形探究即可解决问题．
【考点精析】通过灵活运用矩形的性质，掌握矩形的四个角都是直角，矩形的对角线相等即可以解答此题．
