题目内容
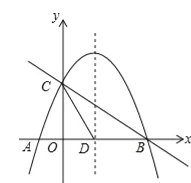
【题目】已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B两点,若m>1,且点A在点B的左侧,OA:OB=1:3
(1)试确定抛物线的解析式;
(2)直线y=kx﹣3与抛物线交于M、N两点,若△AMN的内心在x轴上,求k的值.
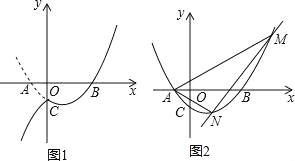
(3)设(2)中抛物线与y轴的交点为C,过点C作直线l∥x轴,将抛物线在y轴左侧的部分沿直线l翻折,抛物线的其余部分保持不变,得到一个新图象,请你结合新图象回答:当直线y=![]() x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
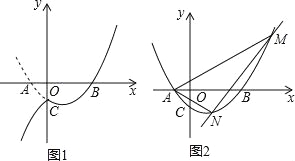
【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1.
x﹣1.
(2)k=﹣3或![]() ;
;
(3)当﹣1<b≤7或b<﹣![]() 时直线y=
时直线y=![]() x+b与新图象只有一个公共点.
x+b与新图象只有一个公共点.
【解析】试题分析:(1)设A(﹣a,0),B(3a,0),根据根与系数关系可得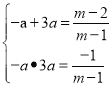 解方程组即可解决问题.
解方程组即可解决问题.
(2)设M(m,km﹣3),N(n,kn﹣3),显然m、n是方程:![]() x2﹣(k+
x2﹣(k+![]() )x+2=0的两根,得到m+n=3k+2,mn=6,再根据直线AM,直线AN两直线与x轴夹角相等,
)x+2=0的两根,得到m+n=3k+2,mn=6,再根据直线AM,直线AN两直线与x轴夹角相等,
即tan∠MAB=tan∠NAB,列出方程,整体代入即可求出k的值.
(3)直线y=![]() x+b与新图象只有一个公共点P(x0,y0)且y0≤7,所以b0≤7,又当直线y=
x+b与新图象只有一个公共点P(x0,y0)且y0≤7,所以b0≤7,又当直线y=![]() x+b经过点C(0,﹣1)时,b=﹣1,所以当﹣1<b≤7时,直线y=
x+b经过点C(0,﹣1)时,b=﹣1,所以当﹣1<b≤7时,直线y=![]() x+b与新图象只有一个公共点,由
x+b与新图象只有一个公共点,由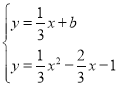 消去y得x2﹣3x﹣3﹣3b=0,当直线y=
消去y得x2﹣3x﹣3﹣3b=0,当直线y=![]() x+b与新图象只有一个公共点时,方程只有相等的实数根,根据△=0,列出方程求出b,由此即可解决问题.
x+b与新图象只有一个公共点时,方程只有相等的实数根,根据△=0,列出方程求出b,由此即可解决问题.
试题解析:(1)∵OA:OB=1:3,
∴可以假设A(﹣a,0),B(3a,0),
则有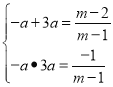 消去a得到3m2﹣16m+16=0,解得m=
消去a得到3m2﹣16m+16=0,解得m=![]() 或4(不合题意舍弃),
或4(不合题意舍弃),
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1.
x﹣1.
(2)设M(m,km﹣3),N(n,kn﹣3),
∵点M、N在抛物线上,则M(m,![]() m2﹣
m2﹣![]() m﹣1),N(n,
m﹣1),N(n,![]() n2﹣
n2﹣![]() n﹣1),
n﹣1),
∴km﹣3=![]() m2﹣
m2﹣![]() m﹣1,kn﹣3=
m﹣1,kn﹣3=![]() n2﹣
n2﹣![]() n﹣1,
n﹣1,
显然m、n是方程:![]() x2﹣(k+
x2﹣(k+![]() )x+2=0的两根,
)x+2=0的两根,
则m+n=3k+2,mn=6,
∵△CMN的内心在y轴上,A(﹣1,0),B(3,0),
∴直线AM,直线AN两直线与x轴夹角相等,
∴tan∠MAB=tan∠NAB
∴![]() ,
,
整理得到,2kmn+K(m+n)﹣3(m+n)﹣6=0,
∴12k+k(3k+2)﹣3(3k+2)=0,
解得k=﹣3或![]() .
.
(3)∵直线y=![]() x+b与新图象只有一个公共点P(x0,y0)且y0≤7,
x+b与新图象只有一个公共点P(x0,y0)且y0≤7,
∴b0≤7,
当直线y=![]() x+b经过点C(0,﹣1)时,b=﹣1,
x+b经过点C(0,﹣1)时,b=﹣1,
∴当﹣1<b≤7时,直线y=![]() x+b与新图象只有一个公共点,
x+b与新图象只有一个公共点,
由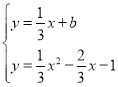 消去y得x2﹣3x﹣3﹣3b=0,
消去y得x2﹣3x﹣3﹣3b=0,
当直线y=![]() x+b与新图象只有一个公共点时,方程只有相等的实数根,△=0,
x+b与新图象只有一个公共点时,方程只有相等的实数根,△=0,
∴9+12+12b=0,
∴b=﹣![]() .
.
∴当b<﹣![]() 时,当直线y=
时,当直线y=![]() x+b与新图象只有一个公共点,
x+b与新图象只有一个公共点,
综上所述,当﹣1<b≤7或b<﹣![]() 时直线y=
时直线y=![]() x+b与新图象只有一个公共点.
x+b与新图象只有一个公共点.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案