题目内容
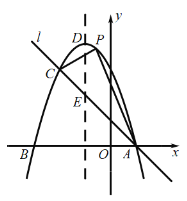
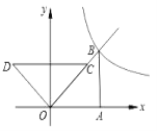
【题目】如图,两个全等的等腰直角三角形放置在平面直角坐标系中,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的解析式;
(2)把![]() 沿射线
沿射线![]() 移动,当点
移动,当点![]() 落在
落在![]() 图象上的
图象上的![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由全等三角形的性质可得AB=OA=OC=OD=![]() ,则可求得B点坐标,代入可求得k的值;
,则可求得B点坐标,代入可求得k的值;
(2)由平移的性质可知DD′∥OB,过D′作D′E⊥x轴于点E,交DC于点F,设CD交y轴于点M,由D点坐标,则可设出D′坐标,代入反比例函数解析式,则可得到关于D点坐标的方程,可求得D点坐标.
解:(1)∵![]() 和
和![]() 为全等的等腰直角三角形,
为全等的等腰直角三角形,![]() ,
,
∴![]() ,
,
∴点![]() 坐标为
坐标为![]() ,
,
代入![]() 得,
得,![]() ;
;
∴反比例函数解析式为![]() ;
;
(2)依题意,得![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,
,
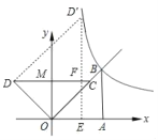
设![]() 交
交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴点![]() 坐标为
坐标为![]() ,
,
设![]() 横坐标为
横坐标为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 在反比例函数图象上,
在反比例函数图象上,
∴![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴![]()

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目