ЬтФПФкШн
ЁОЬтФПЁПвбжЊDЪЧRtЁїABCаББпABЕФжаЕуЃЌЁЯACBЃН90ЁуЃЌЁЯABCЃН30ЁуЃЌЙ§ЕуDзїRtЁїDEFЪЙЁЯDEFЃН90ЁуЃЌЁЯDFEЃН30ЁуЃЌСЌНгCEВЂбгГЄCEЕНPЃЌЪЙEPЃНCEЃЌСЌНгBEЃЌFPЃЌBPЃЌЩшBCгыDEНЛгкMЃЌPBгыEFНЛгкNЃЎ
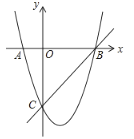
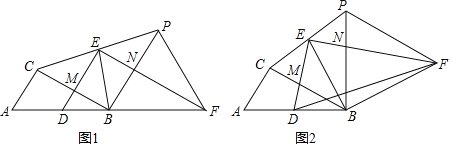
ЃЈ1ЃЉШчЭМ1ЃЌЕБDЃЌBЃЌFЙВЯпЪБЃЌЧѓжЄЃК
ЂйEBЃНEPЃЛ
ЂкЁЯEFPЃН30ЁуЃЛ
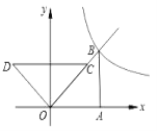
ЃЈ2ЃЉШчЭМ2ЃЌЕБDЃЌBЃЌFВЛЙВЯпЪБЃЌСЌНгBFЃЌЧѓжЄЃКЁЯBFD+ЁЯEFPЃН30ЁуЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйМћНтЮі Ђк30ЁуЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЂйБОЬтжївЊПМВщЭЈЙ§НЧЖШМЦЫуЧѓжЄЦНааЃЌМЬЖјжЄУїЁїCBPЪЧжБНЧШ§НЧаЮЃЌИљОнжБНЧШ§НЧаЮаББпжаЯпПЩЕУНсТлЃЎ
ЂкБОЬтвдЩЯвЛЮЪНсТлЮЊНтЬтвРОнЃЌПМВщЦНааЯпвдМАДЙжБЦНЗжЯпЕФгІгУЃЌИљОнЭЌЮЛНЧЯрЕШПЩЕУBCЁЮEFЃЌгЩЦНааЯпЕФаджЪЕУBPЁЭEFЃЌПЩЕУEFЪЧЯпЖЮBPЕФДЙжБЦНЗжЯпЃЌИљОнЕШбќШ§НЧаЮШ§ЯпКЯвЛЕФаджЪПЩЕУЁЯPFEЃНЁЯBFEЃН30ЁуЃЎ
ЃЈ2ЃЉБОЬтжївЊПМВщИЈжњЯпЕФзіЗЈвдМАДЙжБЦНЗжЯпаджЪЕФгІгУЃЌашвЊбгГЄDEЕНQЃЌЪЙEQЃНDEЃЌСЌНгCDЃЌPQЃЌFQЃЌжЄУїЁїQEPЁеЁїDECЃЈSASЃЉЃЌдђPQЃНDCЃНDBЃЌгЩQEЃНDEЃЌЁЯDEFЃН90ЁуЃЌжЊEFЪЧDQЕФДЙжБЦНЗжЯпЃЌжЄУїЁїFQPЁеЁїFDBЃЈSASЃЉЃЌдйгЩEFЪЧDQЕФДЙжБЦНЗжЯпЃЌПЩЕУНсТлЃЎ
жЄУїЃЈ1ЃЉЂйЁпЁЯACBЃН90ЁуЃЌЁЯABCЃН30Ёу
ЁрЁЯAЃН90ЁуЉ30ЁуЃН60Ёу
ЭЌРэЁЯEDFЃН60Ёу
ЁрЁЯAЃНЁЯEDFЃН60Ёу
ЁрACЁЮDE
ЁрЁЯDMBЃНЁЯACBЃН90Ёу
ЁпDЪЧRtЁїABCаББпABЕФжаЕуЃЌACЁЮDM
Ёр![]()
МДMЪЧBCЕФжаЕу
ЁпEPЃНCEЃЌМДEЪЧPCЕФжаЕу
ЁрEDЁЮBP
ЁрЁЯCBPЃНЁЯDMBЃН90Ёу
ЁрЁїCBPЪЧжБНЧШ§НЧаЮ
ЁрBEЃН![]() PCЃНEP
PCЃНEP
ЂкЁпЁЯABCЃНЁЯDFEЃН30Ёу
ЁрBCЁЮEF
гЩЂйжЊЃКЁЯCBPЃН90Ёу
ЁрBPЁЭEF
ЁпEBЃНEP
ЁрEFЪЧЯпЖЮBPЕФДЙжБЦНЗжЯп
ЁрPFЃНBF
ЁрЁЯPFEЃНЁЯBFEЃН30Ёу
ЃЈ2ЃЉШчЭМ2ЃЌбгГЄDEЕНQЃЌЪЙEQЃНDEЃЌСЌНгCDЃЌPQЃЌFQ

ЁпECЃНEPЃЌЁЯDECЃНЁЯQEP
ЁрЁїQEPЁеЁїDECЃЈSASЃЉ
дђPQЃНDCЃНDB
ЁпQEЃНDEЃЌЁЯDEFЃН90Ёу
ЁрEFЪЧDQЕФДЙжБЦНЗжЯп
ЁрQFЃНDF
ЁпCDЃНAD
ЁрЁЯCDAЃНЁЯAЃН60Ёу
ЁрЁЯCDBЃН120Ёу
ЁрЁЯFDBЃН120ЁуЉЁЯFDCЃН120ЁуЉЃЈ60Ёу+ЁЯEDCЃЉЃН60ЁуЉЁЯEDCЃН60ЁуЉЁЯEQPЃНЁЯFQP
ЁрЁїFQPЁеЁїFDBЃЈSASЃЉ
ЁрЁЯQFPЃНЁЯBFD
ЁпEFЪЧDQЕФДЙжБЦНЗжЯп
ЁрЁЯQFEЃНЁЯEFDЃН30Ёу
ЁрЁЯQFP+ЁЯEFPЃН30Ёу
ЁрЁЯBFD+ЁЯEFPЃН30Ёу