题目内容
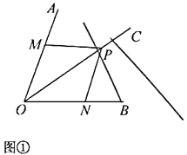
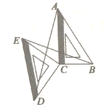
【题目】如图，
是两个直角三角板，其中
，
，若
将直角三角板
绕点
旋转一周，则
的最大值为_______________________．
【答案】
【解析】
如图，在CA取一点J，使得CJ=CB，连接DJ．利用全等三角形的性质证明BE=DJ，推出|AD-BE|=|AD-DJ|≤AJ，求出AJ即可解决问题．
解：如图，在CA取一点J，使得CJ=CB，连接DJ．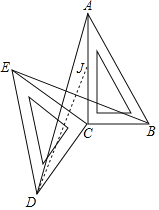
在Rt△ACB中，AB=2，∠CAB=30°，∠ACB=90°，
∴CB=CJ=
AB=1，AC=
BC=，
∵∠ECD=∠BCJ=90°，
∴∠DCJ=∠ECB，
∵CD=CE，CJ=CB，
∴△DCJ≌△ECB（SAS），
∴DJ=BE，
∴|AD-BE|=|AD-DJ|，
∵|AD-DJ|≤AJ，
∴|AD-BE|≤，
∴|AD-BE|的最大值为．
故答案为：．
练习册系列答案
相关题目
